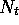Wenn die Peakzählraten in die Größenordnung des Fehler des Untergrunds kommen, läßt sich der Peak nur noch mit einer bestimmten Wahrscheinlichkeit aus dem Untergrund heraus identifizieren. In der Literatur wird in der Regel ein Vertrauensintervall von 95% für die Peakidentifikation angegeben [JEN81].
Energiedispersive Detektoren nehmen Untergrund und Peak
gleichzeitig auf. Um eine statistisch möglichst hohe
Präzision für die Zählrate des Peaks zu erhalten, integriert man
bei Spurenelementen über das 1.2 fache der full width half maximum (FWHM) der
Peakmitte
.
Für die Zählrate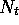 
eines in der Lifetime t aufgenommenen Peaks P folgt damit:
mit U als exakt angenommenem Untergrundwert unter dem
integrierten Peakbereich.
Der Peak P und seine Varianz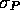 
sind damit
folgendermaßen gegeben:
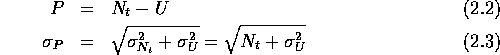
Um die Grenze für die minimal nachweisbaren Zählraten festzulegen,
muß die Streuung des Untergrunds betrachtet werden. Liegt kein Peak
vor, so ist die in Gleichung 2.2 und 2.3 angegebene Zählrate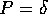 
und ihr Fehler 
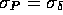nur abhängig von der Streuung des
Untergrunds. Nimmt man einen
poissonverteilten Untergrund an, wird die Zählrate 
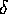normalverteilt
sein mit dem Erwartungswert Null, da die
Gesamtzählraten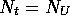 
und der Untergrundwert U sich im Mittel
aufheben [JEN81].
Als Nachweisgrenze für die minimalen
Zählraten eines echten Peaks legt man den Wert fest, bei dem nur noch maximal 5
Prozent der Untergrundschwankungen irrtümlich als Peak identifiziert
werden können und erhält so ein Vertrauensintervall von 95% für die
Peakidentifikation. Da die Zählrate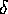 
normalverteilt ist,
erhält man aus der tabellierten Normalverteilung einen Wert von
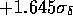für die 5% der Untergrundschwankungen. Für die
minimalen Zählraten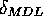 
gilt demnach:
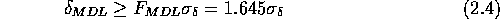
Die minimale Zählrate hängt also von dem Fehler der Untergrundzählraten und dem Fehler des Untergrundwerts unter dem integrierten Peakbereich ab. Abhängig von der Methode der Untergrundbestimmung variiert der Fehler des Untergrundwerts und damit die Nachweisgrenze. Die beiden wichtigen Näherungen für einen genau bestimmten Untergrundwert und einen über die Breite des integrierten Peakbereichs abgeschätzten Untergrundwert werden im Folgenden kurz dargestellt.
Bei einem linearen Untergrundverlauf kann durch Mittelung über eine große Anzahl von Kanälen symmetrisch zur Peakmitte der Untergrundwert sehr genau bestimmt werden. Der Fehler des Untergrundwerts läßt sich dann gegenüber dem Fehler der Gesamtzählrate in Gleichung 2.3 vernachlässigen.
Mittelt man die Untergrundzählrate über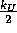 
Kanäle auf
jeder Seite des Peaks, so
ergibt sich der Untergrundwert U unter den 
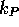Kanälen des
integrierten Peakbereichs zu:
Der Fehler des Untergrundwerts ist dann:
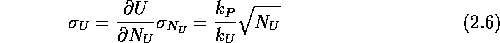
Ist die Anzahl der Kanäle 
, kann man die Streuung des Untergrundwerts gegenüber der
Streuung der Untergrundzählrate in Gleichung 2.3 vernachlässigen und
es ergibt sich:
Für die minimal nachweisbaren Zählrate ergibt sich dann nach Gleichung 2.4 für einen genau bestimmten Untergrundwert folgender Zusammenhang:
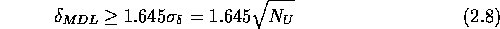
In einem Spektrum mit vielen Linien läßt sich der
Untergrundwert nicht
mehr über eine große Anzahl von Kanälen genau ermitteln. Hier wird
der Untergrundwert
normalerweise über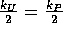 
Kanäle, wobei
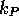die Anzahl der Kanäle im integrierten Peakbereich sind, jeweils recht
und links von der Peakmitte im Untergrundbereich gemittelt. Aus einer
linearen Näherung über die beiden Untergrundbereiche wird der
Untergrundwert im Peakbereich bestimmt. In Gleichungen 2.5
und 2.6 ist dann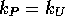 
und nach der Gleichung 2.3 ergibt sich
für die Streuung des Untergrunds:
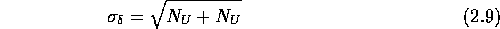
Die Nachweisgrenze für den ungenau bestimmten Untergrundwert ist demnach:
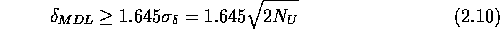
Für die Nachweisgrenze der Röntgenfluoreszenzanalyse an der
Synchrotronstrahlungsquelle ELSA wird Gleichung 2.10 zu Grunde
gelegt, da in der Regel
von einem nicht exakt bestimmbaren Untergrundwert ausgegangen werden muß.
Der Untergrund wird hier über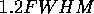 
integriert.
In der Literatur werden noch andere Werte für das Vertrauensintervall, um einen Peak zu identifizieren, angegeben. Tabelle 2.1 gibt einen Überblick über die Faktoren, die sich in Abhängigkeit des angenommen Vertrauensintervalls nach Gleichung 2.4 ergeben. Für die beiden Speziallfälle eines genauen und über den Peakbereich gemittelten Untergrundwerts werden die Peakidentifikationswahrscheinlichkeiten in der linken und rechten Spalte angegeben.
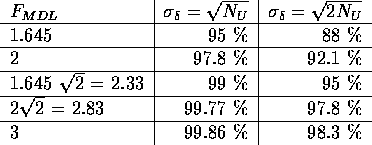
Tabelle 2.1: Die Faktoren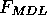 
in Gleichung 2.4, um einen Peak aus den Untergrundschwankungen mit der
entsprechend angebenen Wahrscheinlichkeit, abhängig vom Fehler des Untergrundwerts, zu identifizieren.
Die minimal nachweisbare Zählrate für
ein Vertrauensintervall von 95% kann auch als doppelter Fehler
des Untergrunds
integriert über 2FWHM oder als dreifacher Fehler des Untergrunds
integriert über 1FWHM angegeben werden [MOM78]. Um diese
Nachweisgrenzen besser mit der Gleichung 2.10 vergleichen zu können, wurde der
Integrationsbereich des Untergrunds auf 1FWHM umgerechnet. Vergleicht man die
minimalen Zählraten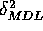 
und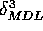 
mit der
oben abgeleiteten Form 
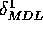, sieht man, daß alle
drei Gleichungen zu recht ähnlich Ergebnissen führen.
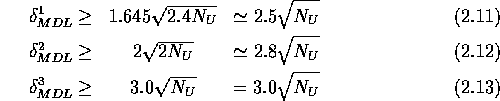
Die sich aus dem Grenzkriterium ergebenden Zählraten müssen noch in Elementkonzentrationen oder bei endlicher Dicke des Targets in absolute Flächenbelegungsdichten umgerechnet werden.
Die Umrechnung geschieht entweder mit Standards, deren Zusammensetzung genau bekannt sind, oder über die FPM. Wegen der erheblichen Absorptionseffekte in dicken Proben müßten die Standards relativ ähnliche Zusammensetzungen aufweisen wie die zu untersuchenden Proben, um die Absorptionseffekte in der unbekannten Probe zu berücksichtigen.
Da das Verfahren über Standards zur Bestimmung der Konzentrationen in einer Probe relativ aufwendig ist, wird die Methode der fundamentalen Parameter zur Berechnung von Konzentrationen und absoluten Flächenbelegungsdichten verwendet.