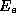Ein einzelnes Elektron der Energie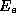 
auf einer Kreisbahn
mit dem Krümmungsradius R strahlt ein kontinuierliches
elektromagnetisches Spektrum nach der Lippmann-Schwinger
Gl. ab [Kun78, Wes83] :
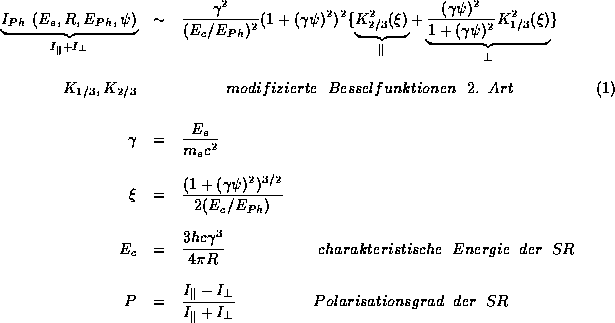
Die Intensität der SR hängt über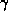 
stark von der Energie
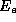der Elektronen und über 
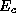vom
Krümmungsradius ihrer Flugbahn R ab.
Beim Betrieb eines Speicherringes zur Erzeugung von SR ist die
Elektronenenergie fest gewählt und der Krümmungsradius der
Elektronenbahn ( i.a. in der horizontalen Ebene ) durch
die Vakuumrohre und die Ablenkmagnete fest vorgegeben.
Die abgestrahlte Intensität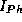 
variiert hierdurch nur noch mit
der Energie der emittierten Photonen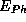 
und deren Emissionswinkel 
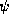in der Vertikalen bezüglich der
horizontalen Bahnebene des Elektrons.
Die spektrale Verteilung der SR zeigt einen starken Intensitätsabfall
zu höheren
Photonenenergien, der sich bei Abstrahlung unter einem Winkel noch
verstärkt [Abb. 7a]. Mit steigender Photonenenergie wird die
SR stärker gebündelt emittiert [Abb. 7b], wodurch
sich das Aufweichen der spektralen Verteilung mit steigendem
Emissionswinkel erklärt. Die Breite dieser Winkelverteilung,
die natürliche Divergenz der SR, nimmt von kleiner Photonenenergie
an rasch mit steigender Energie ab und geht in einen flachen,
schwach abfallenden Bereich bei höheren Photonenenergien über
[Abb. 7c].
Die Gesamtintensität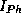 
der SR setzt sich aus einer
parallel (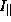 
) zur Bahnebene des Elektrons und
einer senkrecht (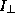 
) dazu polarisierten
Strahlungskomponente zusammen [Gl. 1]. Die parallel polarisierte
Intensität (vorderer Teil des Summanden in der geschweiften Klammer,
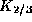) kann, ebenso wie die senkrechte Komponente
(hinterer Teil,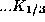 
) separat berechnet werden.
Während die Intensität der parallel polarisierten SR von ihrem Maximum
in der Bahnebene bei Emission unter einem Winkel stark
abfällt, zeigt die senkrecht polarisierte Komponente zwei
symetrisch zur Bahnehene liegende Maxima und eine verschwindende
Intensität in der Elektronenbahnebene [Abb. 7d].
Die insgesamt abgestrahlte spektrale Verteilung wird von der
parallel polarisierten Komponente dominiert, der genaue Polarisationsgrad
der SR in einem Raumwinkelsegment ist von dessen vertikaler Lage und Größe
abhängig. Die in der Beschleunigerebene abgestrahlte
SR ist für die ideal angenommenen Verhältnisse vollständig
parallel polarisiert.
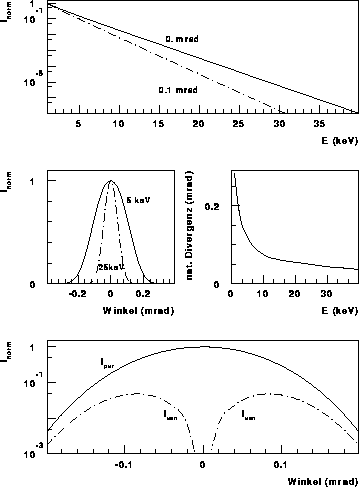
Abb. 7a (oben): normierte Intensität der SR
für die Emissionswinkel 0.mrad und 0.1mrad, aufgetragen gegen die
Photonenenergie.
Abb. 7b (mitte links): Winkelverteilung der SR bei
5 keV und bei 25 keV Photonenenergie
Abb. 7c (mitte rechts): Abhängigkeit der
natürlichen Strahlungsdivergenz (HWHM) der SR-Strahlung von der
Photonenenergie.
Abb. 7d (unten): Winkelverteilung der SR bei 10KeV
für die parallel und die senkrecht polarisierte Komponente
Die Berechnungen sind für eine ideale
Elektronenverteilung mit der Elektronenenergie E = 2.30GeV
und dem Krümmungsradius der Elektronenbahn R = 10.88m durchgeführt.
Die Berechnung der spektralen Verteilung hinter einer, in einem Abstand zum
Quellvolumen stehenden vertikalen Blende erfolgt durch Integration
der Lippmann-Schwinger Gl. über den vertikalen Emissionswinkel.
Hierbei trägt nur der Teil der insgesamt emittierten Strahlung zur
spektralen Verteilung hinter der Blende bei, der die Bedingungen
dieser geometrischen Einschränkung erfüllt.
Die Grenzen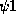 
und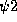 
für die Integration über
den vertikalen Emissionswinkel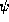 
in Gl. 2 sind durch den Abstand der
Blende vom Quellvolumen, die vertikale Blendenposition und die vertikale
Blendengröße bestimmt.
Die Elektronen in einem Beschleuniger erscheinen i.a. nicht
alle genau auf ihrer Sollbahn, sondern mit einer Ablage ( Offset )
von der Sollebene und unter einem Winkel ( Divergenz )
zu dieser. Die von einem Quellvolumen abgestrahlte spektrale
Verteilung ergibt sich als Überlagerung der Strahlung aller
Elektronen mit individuellem Offset und individueller Divergenz.
Die spektrale Verteilung des insgesamt abgestrahlten Spektrums wird
hierdurch nicht beeinflußt, aber das SR-Spektrum
hinter einer vertikalen Blende ist von der Position und
der Flugrichtung der Elektronen senkrecht zur Beschleunigerebene
abhängig. Da die vertikale Blende, je nach Position und
Flugrichtung der Elektronen für diese unter verschiedenen Winkeln erscheint,
wird die vert. Elektronenverteilung und die vert. Elektronendivergenz
mit der spektralen Verteilung der SR hinter der Blende gekoppelt.
Die Lippmann-Schwinger Gl. muß aber nicht über die vert.
Elektronenverteilung und -divergenz getrennt integriert
werden, sondern beide Strahleigenschaften können durch eine
effektive vertikale Elektronenverteilung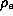 
, die beide Effekte
berücksichtigt, zusammengefaßt werden [Spe90, Pan91]. Unmittelbar hinter
einer festen vertikalen Blende kann wegen der kleinen
Emissionswinkel der SR im betrachteten Bereich (< 1 mrad)
nämlich nicht zwischen den
Auswirkungen der vert. Elektronenverteilung und der
vert. Elektronendivergenz auf die spektrale Verteilung der SR
unterschieden werden. Unter der Annahme einer
effektiven vertikalen Elektronenverteilung vereinfacht sich die
Berechnung der spektralen Verteilung zu :
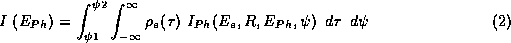
Während die separate Bestimmung von vert. Elektronenverteilung und vert. Elektronendivergenz im Quellvolumen nur schwierig durchführbar ist, läßt sich die effektive vertikale Elektronenverteilung einfach aus der Abrasterung des vertikalen Intensitätsprofils bei bekanntem Abstand Quellvolumen - Blende und definierter Photonenenergie errechnen. Das gemessene Intensitätsprofil muß sich möglichst gut aus der Faltung der, nach der Lippmann-Schwinger Gl. berechneten, idealen Winkelverteilung der SR mit der angenommenen eff. vert. Elektronenverteilung ergeben.