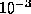Die Betriebsparameter von ELSA beeinflussen über
die eingestellte Elektronenenergie E und den durch die
Beschleunigergeomtrie vorgegebenen Krümmungsradius R direkt
die in den Ablenkmagneten erzeugte SR.
Hierbei werden die Elektronen durch ein zur eingestellten Elektronenenergie
passendes Magnetfeld in den Ablenkdipolen und durch fokusierende
magnetische Quadrupole in der Nähe der Sollbahn in der
horizontalen Beschleunigerebene gehalten.
Die Elektronen laufen dort aber nicht auf starren Bahnen um,
sondern führen horizontale Schwingungen ( Betatronschwingungen
) um ihre Sollbahn aus, wodurch eine horizontale
Elektronenverteilung und eine horizontale Verteilung der
Elektronendivergenz entsteht.
Durch geringe Dejustagen der
magnetischen Felder der zur Strahlführung verwendeten Magnete
werden ebenfalls vertikale Schwingungen anregt [Bry91].
Die Kopplung von horizontalen und vertikalen Schwingungen der Elektronen
und die Wechselwirkung der Elektronen miteinander erzeugen die
im vorhergehenden Abschnitt angesprochene
vert. Elektronenverteilung und vert. Divergenz
der Elektronen. Diese sind auch abhängig von der Position des betrachteten
Quellvolumens in der Magnetstruktur und von den individuellen
Einstellungen der verschiedenen Dipole, Quadrupole und
Korrekturmagnete in ELSA.
Um trotz der vielen verschiedenen, teilweise zeit- und
elektronenstromabhängigen Einflüsse verlässliche Aussagen
über die von dem betrachteten Quellvolumen ausgehende SR zu machen,
ist die Bestimmung der oben eingeführten eff. vert.
Elektronenverteilung während jeder Fluoreszenzmessung unumgänglich.
In Abb. 8 ist die relative Veränderung der spektralen Verteilung
zum einen für die an ELSA zu erwartenden Abweichungen von der
Energie der Elektronen und
dem Krümmungsradius ihrer Bahn gezeigt, zum anderen für mögliche
auftretende Schwankungen in Breite und Lage der eff. vert.
Elektronenverteilung.
Die Elektronenenergie E und der Krümmungsradius
R des Elektronenstrahls im Dipolmagneten sind mit
einer relativen Genauigkeit in der Größenordnung
von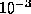 
festgelegt, um den Betrieb eines Speicherringes
zu ermöglichen [Wil92].
Nach Abb. 8 ist die Verschiebung der spektralen Verteilung durch Abweichungen
von Elektronenenergie oder Krümmungsradius vernachlässigbar
gegenüber den Auswirkungen durch die beobachteten Veränderungen
[Kap. 2] der eff. vert. Elektronenverteilung.
Die durchgeführten Abrasterungen der vertikalen SR-Strahlverteilung
zeigen bis auf den störenden Einfluß des Eintrittskollimators
eine gute Übereinstimmung mit der Annahme einer
gaußkurvenförmigen eff. vert. Elektronenverteilung [Abb. 3],
für die der Offset (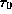 
) und die
Breite (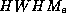 
) der Verteilung die anzupassenden Parameter sind.
In Abb. 9 ist die Abhängigkeit des vertikalen Strahlprofils
der parallel und der senkrecht polarisierten Komponenten der SR
von der Blendenposition für
gaußkurvenförmig angenommene eff. vert. Elektronenverteilungen
verschiedener Breite bei fester Photonenenergie dargestellt.
Mit zunehmender Breite der Elektronenverteilung steigt die Ausdehnung
beider polarisierter Komponenten der SR, die Intensität der senkrecht
polarisierten Komponente ist aber gering im Vergleich zur parallel
polarisierten.
Das vertikale Strahlprofil der SR einer festen Energie
kann trotz des Verlaufs der senkrecht polarisierten Intensität
für die folgenden
Berechnungen näherungsweise als gaußkurvenförmig mit der Breite
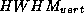angesehen werden.
Hierdurch vereinfacht sich die Entfaltung der gemessenen Strahlprofile
und der natürlichen Strahlungsdivergenz der SR wesentlich.
Während der Offset sich direkt aus den abgerasterten Strahlprofilen
ergibt, kann die Breite der eff. vert. Elektronenverteilung
(
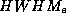) von monochromatisch bei der Photonenenergie E
(mit der natürlichen Strahlungsdivergenz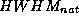 
)
gemessenen Strahlprofilen der Breite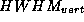 
mit folgender Gleichung berechnet werden :
Die in Gl. 2 einzusetzende Elektronenverteilung wird somit gegeben durch:
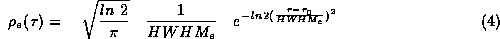
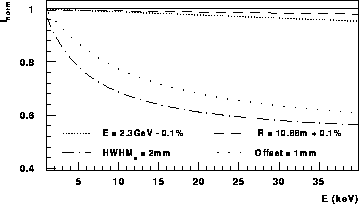
Abb. 8: relative Intensität von berechneten spektralen
Verteilungen mit den angegbenen veränderten Parametern, bezogen
auf eine Verteilung mit der Elektronenenergie E = 2.30 GeV, dem
Krümmungsradius der Elektronenbahn R = 10.88m,
dem Abstand vom Quellvolumen zur Blende d = 16.3m,
einer Blende der vert. Breite b = 0.25mm und einer Breite der
gaußkurvenförmig angenommenen eff. vert. Elektronenverteilung HWHM =
1.0mm ohne Offset der Verteilung
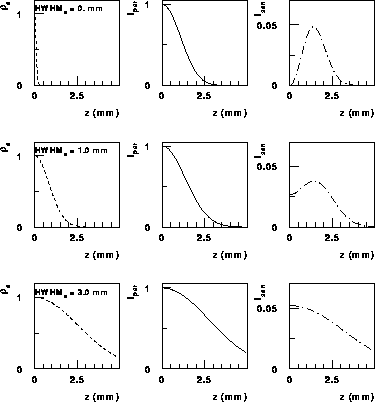
Abb. 9: An der Position der Blende zu erwartende
vertikale Strahlprofile der parallel (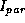
, mitte) und senkrecht
(
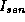, rechts) polarisierten Komponente der SR bei fester
Photonenenergie 10keV mit Veränderung der Breite
(
)
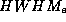einer gaußkurvenförmig angenommenen
eff. vert. Elektronenverteilung (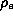
, links).
Die Darstellungen sind für
die Elektronenenergie E = 2.30 GeV, den
Krümmungsradius der Elektronenbahn
R = 10.88m,
den Abstand vom Quellvolumen zur Blende d = 16.3m
berechnet.
Die starke Abhängigkeit der spektralen Verteilung der SR hinter einer
vertikalen Blende von der Breite und Ablage der
eff. vert. Elektronenverteilung ist in Abb. 10 genauer
dargestellt. Mit steigender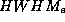 
und steigendem Offset werden die
Verteilungen deutlich weicher, d.h. die Anzahl der hochenergetischen
Röntgenquanten im Spektrum der SR nimmt stärker ab als die der
niederenergetischen. Dies erklärt sich durch die absinkende
natürliche Strahlungsdivergenz der SR mit steigender Energie und die
daraus resultierende Ausblendung hochenergetischer (schwach divergenter)
Anteile. Bei höheren Energien (ab 10 keV) und großer Breite oder
großem Offset unterscheiden sich die nach der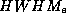 
bzw. dem
Offset parametrisierten Kurven fast nur noch durch
einen reinen Intensitätsfaktor, die spektrale Verteilung
in diesem Bereich ist annähernd gleich. Die hinter der vertikalen Blende
sichtbare eff. vert. Elektronenverteilung gleicht sich einer breiten
Rechteckverteilung mit lediglich unterschiedlicher Höhe an.
Aus den Darstellungen ist auch ersichtlich, daß die spektrale
Verteilung der SR in dem betrachteten Bereich bei großer Breite
unemfindlicher auf eine Veränderung der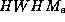 
und bei kleinem Offset
unempfindlicher auf eine Veränderung von diesem reagiert.
Abb. 11a stellt die Abhängigkeit der spektralen Verteilung von
der Breite der Elektronenverteilung (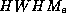
) bei verschiedenem
Offset am Beispiel des Verhältnisses zweier SR-Intensitäten
niedriger und hoher Photonenenergie dar. Die empfindliche
Abhängigkeit dieses Verhältnisses bei keinen Werten der
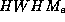verschwindet auch bei groß gewähltem Offset fast
vollständig für ausgedehnte eff. vert. Elektronenverteilungen.
Der Polarisationsgrad der SR hinter einer vertikalen Blende
nimmt zu kleinen Photonenenergien hin ab und fällt mit wachsender
Breite der eff. vert. Elektronenverteilung (ohne Offset) auf
einen Grenzwert des weiterhin energieabhängigen Polarisationsgrades
[Abb. 11b].
Dieses Verhalten des Polarisationsgrades beruht, ähnlich dem der
spektralen Verteilung, wieder auf der
Angleichung der durch die vertikale Blende sichtbaren
eff. vert. Elektronenverteilung an eine Rechteckverteilung.
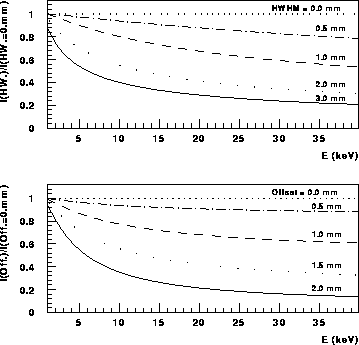
Abb. 10a (oben): relative Intensität von
berechneten spektralen Verteilungen für verschiedene 
der
eff. vert. Elektronenverteilung, bezogen auf eine ideale Verteilung ohne Offset
Abb. 10b (unten): relative Intensität von berechneten spektralen
Verteilungen für verschiedene Werte des Offset der
eff. vert. Elektronenverteilung, bezogen auf eine Verteilung mit
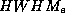= 1.0mm ohne Offset
Die Parameter der Berechnungen betragen für
die Elektronenenergie E = 2.30 GeV, den
Krümmungsradius der Elektronenbahn R = 10.88m,
den Abstand vom Quellvolumen zur Blende d = 16.3m
und einer Blende der vert. Breite b = 0.25mm
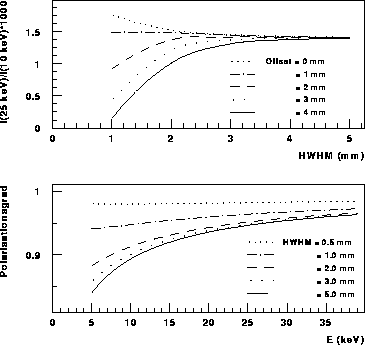
Abb. 11a (oben): Verhältnis der
SR-Intensitäten bei 10keV und 25keV bei verschiedenem Offset,
aufgetragen gegen die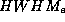 
einer gaußkurvenförmigen eff. vert. Elektronenverteilung.
Abb. 11b (unten): Polarisationsgrad der SR für
verschiedene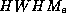 
der eff.
vert. Elektronenverteilung ohne Offset der Elektronenverteilung.
Berechnet für Verteilungen mit der Elektronenenergie E = 2.30 GeV, dem
Krümmungsradius der Elektronenbahn R = 10.88m,
dem Abstand vom Quellvolumen zur Blende d = 16.3m,
und einer Blende der vert. Breite
b = 0.25mm