4.3 Datenbearbeitung

   

4.3.1 Korrektur der Positionierungsfehler

  Die Aufnahme der Meßwerte erfolgt in der Bewegung. Da der Meßvorgang eine gewisse Zeit in Anspruch nimmt, entspricht die Position, die dem Meßwert zugeordnet wird, nicht der tatsächlichen Position des Meßwertes. Es treten Bewegungsartefakte auf, die einer Korrektur bedürfen. Geht man die Linien immer in der selben Richtung ab, so ergibt sich ein Versatz der Positionen der Meßwerte in Laufrichtung. Dieser ist umso größer, je größer die Geschwindigkeit ist. Die Meßwerte sind fälschlicherweise zu höheren y-Werten hin verschoben. Mißt man bidirektional, so ergibt sich das typische Reißverschlußmuster, das vom Wechsel der Laufrichtung hervorgerufen wird. Diese Fehler müssen korrigiert werden, um ein naturgetreues Abbild der lokalen magnetischen Flußdichte zu erhalten.

  
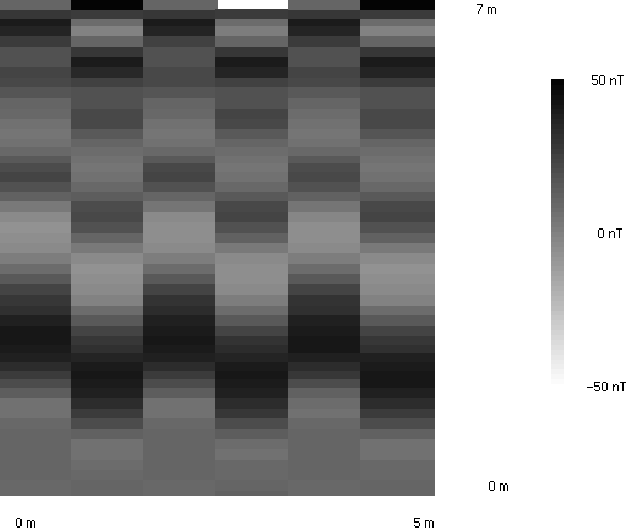
Abbildung 4.1: Positionierungsfehler des Meßgeräts bei bidirektionaler Messung

  
Abbildung 4.2: Unterbrecher im Maßstab 1:1

In Abbildung 4.1 sieht man eine unkorrigierte Testmessung. Die Linien wurden in Nord-Süd-Richtung gelegt und sind lang. Die x-Koordinaten in Abbildung 4.1 spielen keine Rolle, da ein und dieselbe Linie mehrmals bidirektional mit dem Meßwagen abgefahren wurde. Das Meßintervall betrug , die Geschwindigkeit betrug . Dies wurde aus den ursprünglichen Daten ermittelt, die die Zeitpunkte der Markenereignisse enthalten. Deutlich zeigt sich das typische Reißverschlußmuster. Die durchschnittliche Verschiebung beträgt . Sie kann aus den unkorrigierten Meßwerten ermittelt werden, indem man mit Hilfe der Positionskreuze die Koordinaten der Anomalien bestimmt und dann die Differenz der auseinandergerissenen Lineamente ermittelt. Da der Wagen nach Erreichen des Linienendes nicht gedreht wurde, sondern rüchwärts zurückgezogen wurde, um den bereits in Abschnitt 3.1.4 angesprochenen Heading Error zu vermeiden, ist ein Teil dieses Positionierungsfehlers auf die Geometrie des Unterbrechers des optoelektronischen Impulsgebers zurückzuführen. Wie man in Abbildung 4.2 sehen kann, verschiebt sich die Positionierung um 1/4 des Radumfanges, wenn der Wagen nicht gedreht, sondern einfach zurückgezogen wird. Bei einem Radumfang von entspricht dies einem zusätzlichen Positionierungsfehler von . Der Effekt, der auf die Meßdauer des Gerätes zurückzuführen ist, beträgt hier also . Die Messung wurde mit einem Meßintervall von wiederholt. Die Durchschnittsgeschwindigkeit betrug ebenfalls . Es wurde ein Positionierungsfehler von festgestellt. Der Effekt des Meßgerätes auf den Positionierungsfehler beträgt nun folglich . Es zeigt sich also, daß sich die Verschiebung mit doppeltem Meßintervall bei gleichbleibender Geschwindigkeit ebenfalls verdoppelt. Da jede Linienrichtung die Hälfte zum Positionierungsfehler beiträgt, ergeben sich bei einem Meßintervall von eine Meßdauer von und bei einem Meßintervall von eine Meßdauer von . Man kann also davon ausgehen, daß die Meßdauer jeweils der Hälfte des Meßintervalls entspricht. Die Korrektur des Positionierungsfehlers der Größe erfolgt, indem auf der Hinrichtung von y subtrahiert und auf der Rückrichtung der gleiche Betrag addiert wird. Abbildung 4.3 zeigt dieselbe Messung, jedoch nach der Korrektur durch XMAGCAL. Man kann sehr gut erkennen, daß eine Korrektur notwendig ist und den optischen Eindruck stark verbessert. Trotzdem ist im unteren Teil der Abbildung noch eine kleine Abweichung vorhanden. Diese kann durch Geschwindigkeitsveränderungen erklärt werden, da sich an dieser Stelle eine Erhebung befindet, die den Meßwagen langsamer werden läßt.

  
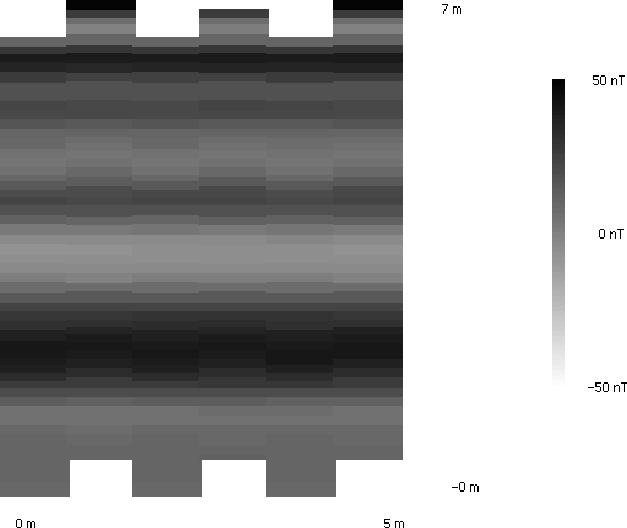
Abbildung 4.3: Meßwerte nach der Korrektur des Positionierungsfehlers

 

 

4.3.2 Korrektur des Heading Errors

  Die Entstehung des Heading Errors wurde bereits in Abschnitt 3.1.4 erläutert. Die Größenordnung dieses Fehlers liegt im Bereich um . Er hängt von der Größe des Magnetfeldes ab und müßte daher durch Multiplikation mit einem Faktor korrigiert werden. Da sich jedoch die einzelnen Faktoren in unserem Meßbereich um weniger als die Meßgenauigkeit in Gradiometeranordnung unterscheiden, erfolgt die Korrektur additiv. Um diesen Fehler zu demonstrieren, wurde eine Testmessung durchgeführt (Abb. 4.4). Hierbei wurden die Linien in Nord-Süd-Richtung ausgerichtet und eine

  
Abbildung 4.4: Heading Error

Linienlänge von gewählt. Es wurden 9 Linien im Abstand von vermessen. In einem ersten Schritt kann man sich die Histogramme der Hin- und Rückrichtungen getrennt ansehen (Abb. 4.5). Hier stellt man meist eine Verschiebung der Histogrammschwerpunkte fest. Nun wählt man sich ein geeignetes Intervall, das nur den magnetischen Untergrund und keine Anomalien enthält. Für dieses Intervall läßt man sich die Mittelwerte der einzelnen Linien berechnen (Abb. 4.6) und kann dann anhand dieser Daten entscheiden, um welchen Betrag die Linien korrigiert werden sollen. Die durchschnittliche Differenz zwischen den beiden Linienrichtungen beträgt hier .

  
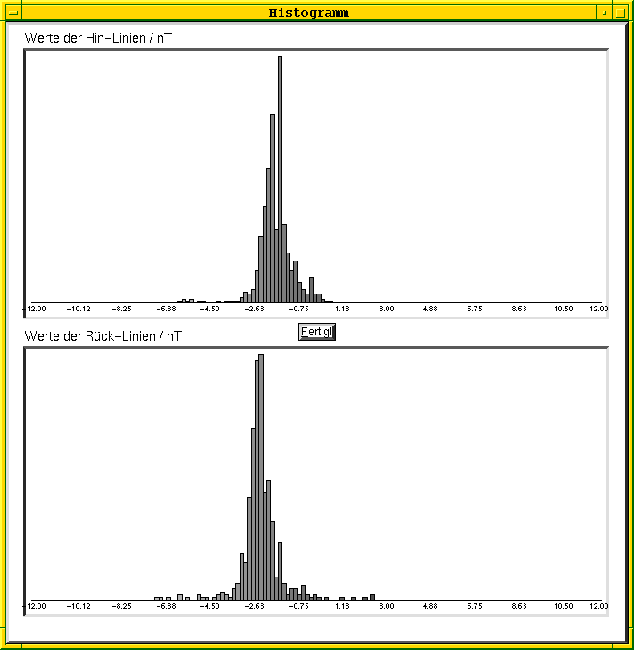
Abbildung 4.5: Histogrammdarstellung der unkorrigierten Meßwerte

  
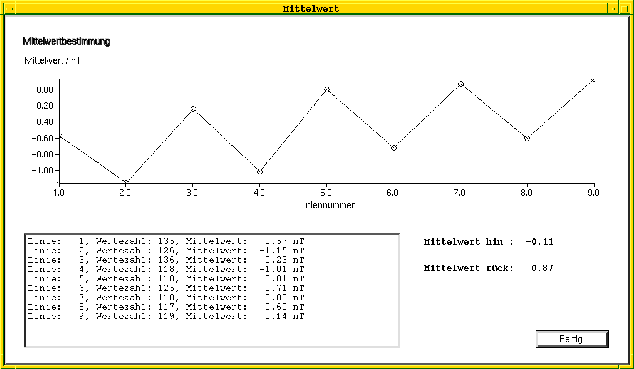
Abbildung 4.6: Mittelwertdarstellung der unkorrigierten Meßwerte

  
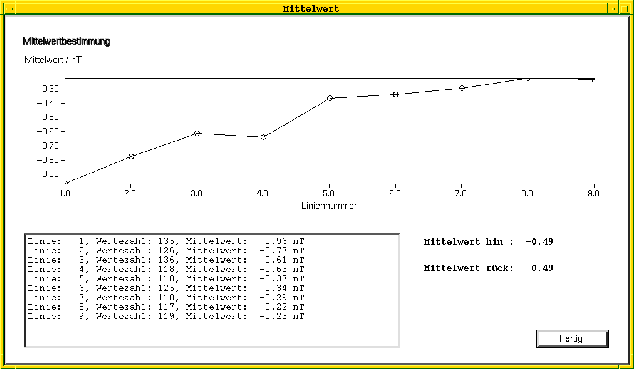
Abbildung 4.7: Mittelwertdarstellung der korrigierten Meßwerte

In diesem Beispiel erkennt man sehr schön die Unterschiede in den Mittelwerten. Es ist aber auch eine steigende Tendenz im Magnetfeld von Linie zu Linie zu beobachten. Dieser lokale Gradient läßt sich auf ein Haus zurückführen, das sich etwa westlich dieses Testfeldes befindet. Von den Meßwerten der Linien der Hinrichtung wird subtrahiert, zu den Meßwerten der Rückrichtung wird der gleiche Betrag addiert, so daß die Niveaus der Linien aneinander angepaßt wurden. Trennt man die Datensätze, so kann man diese Anpassung natürlich auch für Teilbereiche bis hin zu einzelnen Linien vornehmen. Dies ist z.B. sinnvoll, wenn sich während der Messung ein Sensor leicht verstellt hat. Schaut man sich erneut die Linienmittelwerte (Abbildung 4.7) und das Histogramm (Abbildung 4.8) an,

  
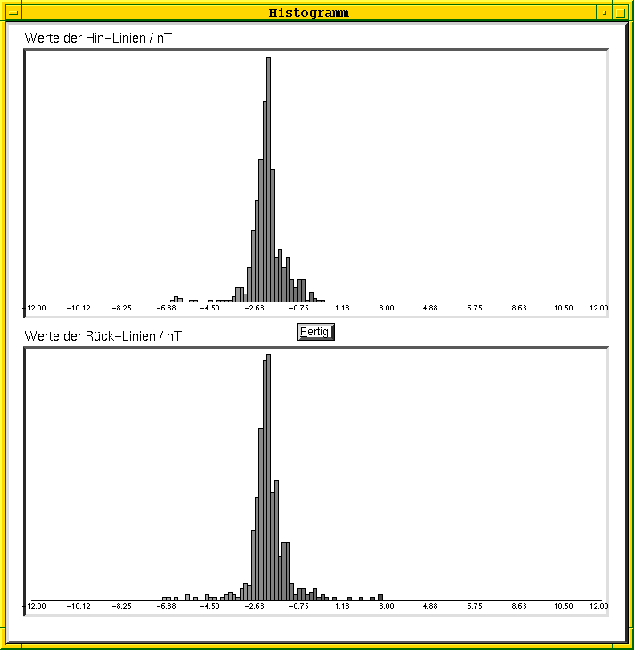
Abbildung 4.8: Histogrammdarstellung der korrigierten Meßwerte

so erkennt man an diesen Werten, daß die Korrektur erfolgreich war. Die Linien wurden einander angepaßt. Optisch wird dies in Abbildung 4.9 deutlich. Die Helligkeitsunterschiede zwischen benachbarten Linien sind verschwunden. Der Positionierungsfehler wurde bereits vorher korrigiert, um den Einfluß des Heading Errors besser zu erkennen. Jetzt sind die zahlreichen kleinen Anomalien gut zu erkennen, die höchstwahrscheinlich auf den basaltsteinhaltigen Boden des Testfeldes in Vettelschoß bei Linz am Rhein zurückzuführen sind.

  
Abbildung 4.9: Meßwerte nach der Korrektur des Heading Errors

 

4.3.3 Weitere Datenmanipulationen

Offset

    Prospektiert man ein großes Feld an mehreren Tagen, kann es zu einem allgemeinen Offset im Gradienten der magnetischen Flußdichte kommen. Die Gründe hierfür wurden bereits in Abschnitt 3.1.3 erläutert. Möchte man diese Daten im selben Graustufenplot darstellen, so unterscheiden sich die verschiedenen Messung in ihrer Helligkeit, so daß eine Anpassung vorgenommen werden muß. Hierzu addiert das Programm zu den Meßwerten den angegebenen Betrag hinzu, und man kann so die Niveaus der einzelnen Messungen aneinander angleichen.

Multiplikation

XMAGCAL berechnet den Gradienten immer mit einem Sensorabstand von . Hat man nun aber einen anderen Sensorabstand gewählt, so ist man mit dieser Funktion des Programms in der Lage, die Daten mit einem Faktor zu multiplizieren, um den Gradienten exakt wiederzugeben. Mißt man beispielsweise mit einem Abstand von , so multipliziert man den gesamten Datensatz mit 0.5, und hat den Gradienten korrekt in nT/m angegeben. Desweiteren kann es vorkommen, daß die Anschlüsse des oberen und des unteren Sensors am Meßgerät vertauscht werden. Dies kann man korrigieren, indem man den Datensatz später mit -1 multipliziert. Somit erhält man die korrekte Darstellung von positiven und negativen Gradienten.