Elektromagnetische Strahlung erfährt beim Einfall auf eine Grenzschicht
zweier unterschiedlicher Medien eine Änderung in ihrer
Fortpflanzungsgeschwindigkeit. Trifft sie in einem Winkel auf, der vom Lot auf
der Grenzschicht abweicht, führt dies zu einer Änderung der
Fortpflanzungsrichtung. Die Brechung des Einfallswinkels 
wird durch
das Snelliussche Brechungsgesetz beschrieben [Bor64]:
Hierbei sind n und n' die Brechungsindizes der beiden Medien, und
, 
die jeweiligen Winkel des Wellenvektors 
bezüglich des Normalvektors der Grenzfläche.
Im folgenden soll statt dem Winkel der Winkel 
bezüglich der Grenzfläche betrachtet werden.
Ein Teil der Strahlung wird reflektiert. Der Reflexionswinkel entspricht
dem Einfallswinkel. Unter der Reflektivität versteht man hierbei das
Verhältnis der
Intensitäten der reflektierten und der einfallenden Strahlung.
Ist n > n', so spricht man in der Optik vom Übergang von einem optisch dichteren in ein optisch dünneres Medium. In diesem Fall gibt
es einen kritischen Winkel:
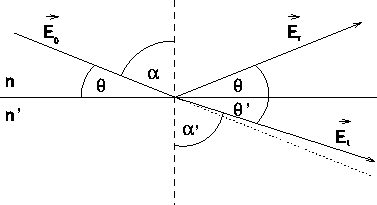
Abbildung: Brechung elektromagnetischer Strahlung beim Übergang zwischen zwei
Medien
Bei diesem Einfallswinkel ergibt sich ein Brechungswinkel von 
. Der gebrochene Lichtstrahl läuft entlang der Grenzfläche. Ist der
Einfallswinkel flacher, so ergibt sich für 
kein realer Wert
mehr. Die
Strahlung tritt nicht in das zweite Medium ein und wird vollkommen reflektiert
[Bor64].
A. H. Compton wies 1922 eine solche Totalreflexion auch bei Röntgenstrahlung
nach [Com22]. Im Gegensatz zum Brechungsindex des sichtbaren Lichts ist
der Realteil des Brechungsindex in Materie für Röntgenstrahlung kleiner als
1.
Die positive Werte 
und 
hängen in erster Linie von der
Energie der Strahlung und von Ordnungszahl und Dichte des Mediums
ab. Typischerweise liegt im Energiebereich der Röntgenstrahlung bei
etwa 
. Der Imaginärteil ist im allgemeinen etwa
um einen Faktor 10 - 1000 kleiner. Da das 'dichtere' Medium im Energiebereich
der Röntgenstrahlung das Vakuum bzw. die Luft ist, tritt die Totalreflexion
beim Übergang von Luft in ein festes Medium auf.
