Divergenz bei endlicher Elektronenstrahlbreite

Die bisherigen Betrachtungen gingen von einer idealen Elektronenbahn im Beschleuniger, dem sogenannten Orbit, aus. Tatsächlich weichen die einzelnen Elektronenbahnen jedoch aufgrund der Betatronschwingungen vom Orbit ab. Die Amplituden der Betatronschwingungen und nehmen für jeden Punkt s der Elektronenbahn andere Werte an. In guter Näherung kann von einer Gaußschen Normalverteilung der einzelnen Bahnen um den Orbit herum ausgegangen werden [Wil92]. Sowohl in vertikaler als auch in horizontaler Richtung ergibt sich somit eine endliche Elektronenstrahlbreite:

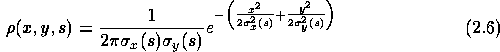
Hierbei ist die transversale Aufenthaltswahrscheinlichkeit eines Elektrons. Mit dem Faktor multipliziert (N - Anzahl der Elektronen, e - Ladungsdichte) ergibt sich hieraus die transversale Ladungsdichte. Bei und handelt es sich um die horizontalen und vertikalen Elektronenstrahlbreiten, d.h. die Abstände von der Strahlachse, bei denen die Elektronendichte auf 1/e abgefallen ist.
Zur Elektronenstrahlbreite kommt die Strahldivergenz hinzu, die ebenfalls als normalverteilt angenommen werden kann. Die Elektronenverteilung und die Strahldivergenz bilden mit ihren Standardabweichungen für die horizontale und vertikale Richtung jeweils Phasenellipsen, die die Teilchenbewegung beschreiben. Die Flächen dieser Phasenellipsen werden üblicherweise mit und angegeben, wobei und als Emittanz des Gesamtstrahls bezeichnet werden. Diese Emittanzen sind konstant über die gesamte Elektronenbahn. Mit der Amplitude der Betatronschwingung ergibt sich für die horizontale Strahlbreite

und für die Standardabweichung der Strahldivergenz bei x = 0:

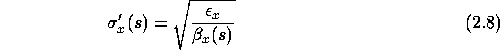
Um das tatsächliche Spektrum der Synchrotronstrahlung zu berechnen, müßte daher die Schwingergleichung mit der vertikalen Strahlbreite und Divergenz gefaltet werden . Für die horizontale Richtung ergeben sich zudem Abweichungen von der erwarteten Rechteckverteilung und Abschattungseffekte.
Betrachtet man Breite und Divergenz des Strahls im Phasenraum, so können die beiden Größen jeweils zu einer horizontalen bzw. vertikalen effektiven Elektronendichte bzw. zusammenfaßt werden [Wil92]. Die tatsächliche Divergenz der Synchrotronstrahlung ergibt sich somit aus der Faltung der effektiven Elektronenverteilungen mit den jeweiligen natürlichen Divergenzen.

Reale vertikale Divergenz

Setzt man eine vertikale Blende der Breite im Abstand D vom Quellpunkt in den Strahl, so läßt sich die Intensität der Strahlung, die mit einem Winkel zur Ebene abgestrahlt wird, wie folgt berechnen:

Hierbei entspricht der aus der Schwingergleichung berechneten Synchrotronstrahlungsintensität für die Energie E. Mit läßt sich ein Versatz der Blende gegenüber der Beschleunigerebene berücksichtigen. Unberücksichtigt bleibt hierbei zunächst die horizontale Winkelverteilung. In der Annahme einer großen horizontalen Blende geht lediglich der horizontale Öffnungswinkel ein.

  
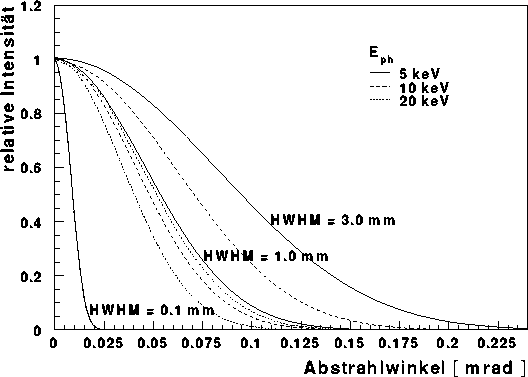
Abbildung: Vertikale Divergenz bei endlicher Elektronenstrahlbreite - Aufgetragen ist hier für drei verschiedene Energien der Synchrotronstrahlung deren Divergenz hinter einer eingestellten Blende von . Hierbei wurden verschiedene effektive vertikale Elektronenstrahlbreiten betrachtet. Die jeweilige HWHM des Elektronenstrahls steht an der Divergenzkurve für 5 keV, da sich hier die Auswirkungen am ehesten bemerkbar machen.

In Abbildung ist für verschiedene Elektronenstrahlbreiten die vertikale Divergenz der Synchrotronstrahlung hinter einer Blende von aufgetragen. Dabei wurden drei unterschiedliche Energien betrachtet. Die Divergenz ist umso größer, je kleiner die Energie der Strahlung ist.
Betrachtet man statt des Winkels die vertikale Position an einem Bezugspunkt im Strahlrohr, so läßt sich für diesen Bezugspunkt ein Strahlprofil berechnen. Vor jeder Meßreihe werden an der Targetposition vertikale Strahlprofile aufgenommen, indem eine horizontal offene Blende durch den Strahl gefahren wird und dabei die Fluoreszenzstrahlung eines Silbertargets beobachtet wird. Bei bekannter natürlicher Divergenz für die Energie der Ag Linie kann so die effektive vertikale Elektronenstrahlbreite abgeschätzt werden [Hei95]. Zusätzlich werden während den Messungen ständig über ein Diodenarray vertikale Strahlprofile aufgenommen. Die spektrale Verteilung der Synchrotronstrahlung, die durch die vertikale Blende gelangt, hängt wesentlich von der vertikalen effektiven Elektronenstrahlbreite ab. Diese kann sich aber durchaus während eines Speicherzyklus ändern [Hei94].

Reale horizontale Divergenz

  Die horizontale Winkelverteilung sollte im Gegensatz zur vertikalen nicht energieabhängig sein. Dies wurde durch Messungen am SYXRF Meßplatz auch verifiziert [Hei95]. Zu einer Abschätzung der Abhängigkeit der horizontalen Divergenz von der Elektronenverteilung wurde eine Verlagerung der idealen Kreisbahn betrachtet. Dabei wurde eine Änderung des Radius in der Beschleunigerebene vernachlässigt. Dies ist berechtigt, wenn ein konstantes Dipolfeld im Ablenkmagneten und eine gleichbleibende Elektronenenergie vorausgesetzt wird. Abbildung zeigt die Auswirkungen einer Verschiebung der Kreisbahn senkrecht zum Mittelpunktstrahl des idealen Orbits. Die Tangenten der verlagerten Kreisbahn gehen jeweils in einem anderen Winkel durch die Blende und die Auftreffpunkte auf die Targetebene verschieben sich. Eine Verteilung solcher Kreisbahnen um die Idealbahn führt zu einer Verschmierung der horizontalen Verteilung in der Targetebene.

  
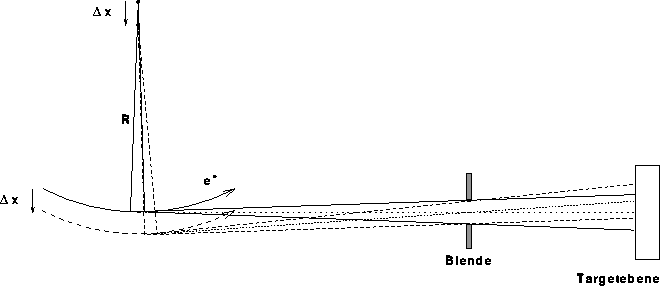
Abbildung: Auswirkung einer horizontalen Verschiebung der Elektronenkreisbahn

Jede Elektronenbahn für sich ergibt eine Rechteckverteilung der Synchrotronstrahlung hinter der Blende. Diese Rechteckverteilungen strahlen allerdings unter verschiedenen Winkeln durch die Blende und überlagern sich in der Targetebene.
In einem einfachen Modell kann die horizontale Verschiebung des Quellpunkts senkrecht zum Mittelpunktstrahl des Orbits betrachtet werden. Hierbei werden unterschiedliche Öffnungswinkel, bedingt durch eine Verlagerung des Quellpunkts bezüglich der Eintrittsblende, vernachlässigt. Für eine Elektronendichte ergibt sich damit folgende Winkelverteilung hinter einer Blende der Breite :

 

Zu beachten ist hierbei, daß nicht von abhängt. Desweiteren ist bei einem Einblendensystem auch kein Versatz zu berücksichtigen, wie bei der vertikalen Divergenz.

  
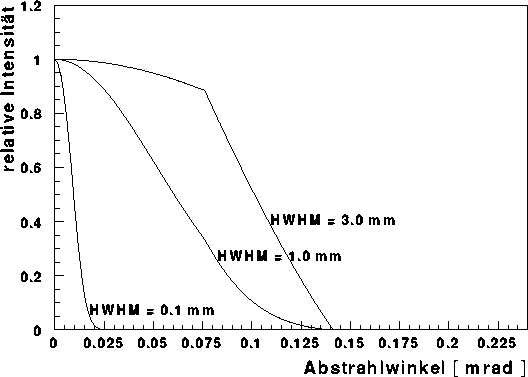
Abbildung: Horizontale Divergenz bei endlicher Elektronenstrahlbreite - Analog zu Abbildung ist hier die berechnete horizontale Divergenz hinter einer Blende von aufgetragen. Die Elektronenstrahlbreite wurde hierbei nach Gleichung betrachtet. Im Gegensatz zur vertikalen Divergenz ist die horizontale nicht energieabhängig. Bei großen Elektronenstrahlbreiten sieht man den Einfluß der horizontalen 1 mm Eintrittsblende.

In Abbildung sind nach Gleichung analog zu Abbildung horizontale Divergenzen für verschiedene Elektronenstrahlbreiten aufgetragen. Die Divergenz ist in diesem Fall nicht energieabhängig. Zudem ist bei großen Elektronenstrahlbreiten der Einfluß der horizontalen Eintrittsblende zu erkennen.
Analog zu den Messungen des vertikalen Strahlprofils werden vor jeder Meßreihe horizontale Strahlprofile aufgenommen. Auf eine Überwachung während der Messungen kann jedoch verzichtet werden, da die horizontale Winkelverteilung keinen Einfluß auf das anregende Spektrum hat. In Abbildung ist ein Vergleich eines aufgenommenen Strahlprofils mit nach berechneten Strahlprofilen zu sehen. Das experimentelle Strahlprofil wurde mit einem Draht aufgenommen, der bei offener horizontaler Blende duch den Strahl gefahren wurde. Hierbei wurden unterschiedliche Elektronenstrahlbreiten angenommen. Das Plateau in der Mitte wird bei größeren Elektronenstrahlbreiten schmaler und das Strahlprofil wird insgesamt breiter. Dies führt zu einem Intensitätsverlust an der Nullposition. Setzt man eine zweite kleinere Blende hinter die Eintrittsblende, ist die Intensität der Strahlung, die durch diese Blende kommt, kleiner als bei einer idealen Rechteckverteilung zu erwarten wäre. In der Tat wird bei den üblichen SYXRF Messungen ein Intensitätsverlust beobachtet, der anscheinend von den Maschineneinstellungen des Beschleunigers abhängt [Hei95].

  
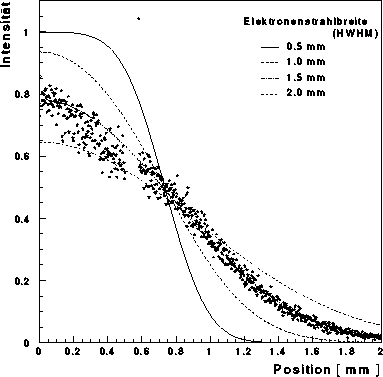
Abbildung: Horizontales Strahlprofil - Mit einem Kupferdraht, der bei offener horizontaler Blende durch den Strahl gefahren wurde, ist ein horizontales Strahlprofil aufgenommen worden. Nach Gleichung wurden für verschiedene Elektronenstrahlbreiten horizontale Strahlprofile berechnet. Das aufgenommene Strahlprofil entspricht einer HWHM von etwa 1.5 mm.

Die maximale horizontale Divergenz des Strahls läßt sich anhand der beiden Blenden einfach abschätzen. Ein Zweiblendensystem aus der Eintrittsblende von 1 mm und einer eingestellten Blende von in 4.3 m Entfernung würde einen größtmöglichen Öffnungswinkel von zulassen (vgl. Abbildung ).
Das Strahlrohr ist allerdings ein komplizierteres Blendensystem. So ist der Strahl schon durch die Vakuumrohre an sich (NW-40: 40 mm Durchmesser) und durch Vakuumfenster zwischen den einzelnen Meßaufbauten in seiner Ausdehnung eingeschränkt. So kann es zu Abschattungseffekten kommen oder im Extremfall, wie es bei einer Dejustage des Elektronenstrahlrohrs im Ablenkmagneten der Fall war, zu einer totalen Ausblendung.
Die Betrachtung der horizontalen Verschiebung des Quellpunkts in der Ebene senkrecht zur Abstrahlrichtung ist lediglich eine Modellrechnung, die dazu dient, den Einfluß der horizontalen Elektronenverteilung auf die Strahldivergenz abzuschätzen. Tatsächlich wird sich jedoch der Abstand des Quellpunkts von der Eingangsblende bei einer Verlagerung der Elektronenbahn verändern. Da der Radius der Kreisbahn in etwa dem Abstand zur Eingangsblende entspricht, liegt die Verlageung des Quellpunkts bezüglich der Blende in der gleichen Größenordung, wie die Verlagerung der Elektronenbahn und kann somit vernachlässigt werden. Die Divergenz des Elektronenstrahls kann ebenfalls als Verlagerung der Kreisbahn betrachtet werden unter der Voraussetzung, daß der Radius, der durch das Dipolfeld und die Energie der Elektronen gegeben ist, für alle Elektronenbahnen gleich ist.