betrachtet.
An einer Grenzfläche unterscheidet man zwischen dem einfallenden Strahl
, dem reflektierten Strahl 
und dem transmittierten Strahl 
,
der unter einem gebrochenen Winkel in das zweite Medium eindringt. Für einen
Abstand z zur Oberfläche ergeben sich dann folgende Beziehungen:
Hierbei sind 
und 
die Komponenten der jeweiligen
Wellenvektoren 
parallel und senkrecht zur Oberfläche. Für die
x-Komponente gilt die Randbedingung 
.
Man unterscheidet zwischen senkrecht und parallel zur Einfallsebene
polarisierter Strahlung ( 
- und 
-Polarisation), wobei die
Einfallsebene durch die Einfallsrichtung und den Normalvektor auf der
Grenzfläche aufgespannt wird. Reflexion und Transmission für senkrecht
polarisierte Strahlung lassen sich dann wie folgt berechnen :
und für parallel polarisierte Strahlung:
Betrachtet man den Fall, daß Röntgenstrahlung von Luft in ein festes Medium eintritt, kann 
und 
gesetzt werden. Außerdem läßt sich 
durch Gleichung 
ausdrücken. Es ergibt sich für einen Einfallswinkel 
:
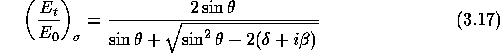
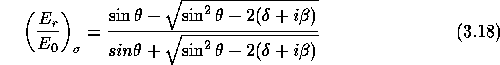
bzw:
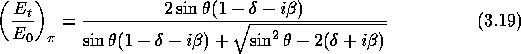
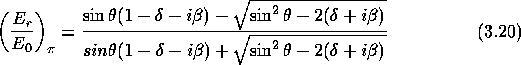
Die entsprechenden Intensitäten der Strahlung ergeben sich mit 
aus dem Betragsquadrat der Amplituden. Somit erhält man für das Reflexionsvermögen von Röntgenstrahlung beim Übergang vom Vakuum in ein Medium folgende Ausdrücke [Hen93]:
wobei:
Das Verhältnis von senkrechter zu paralleler Polarisation ist für kleine Einfallwinkel nahezu 1, so daß im folgenden nur noch die Reflexion für senkrecht polarisierte Strahlung betrachtet wird.
In Abbildung ist für verschiedene Reflektoren die Reflektivität
für eine Energie von 20 keV gegen den Einfallswinkel aufgetragen.
Die Abhängigkeit des kritischen Winkels von der Kernladungszahl des
Reflektormaterials wird deutlich.
Die Form der einzelnen Kurve hängt außerdem vom Verhältnis
zu 
ab. Bei Vernachlässigung von würde man für die
Reflektivität über den gesamten Winkelbereich unterhalb des kritischen
Winkels den Wert 1 [Par54] erwarten. Da jedoch ein Teil der Strahlung im
Reflektor absorbiert wird, liegt die Reflektivität unter 1 und die Kurve ist
abgeflacht. Je kleiner das Verhältnis 
ist, desto größer ist
die Reflektivität unterhalb des kritischen Winkels und desto schärfer
erscheint der Übergang beim kritischen Winkel für Totalreflexion.
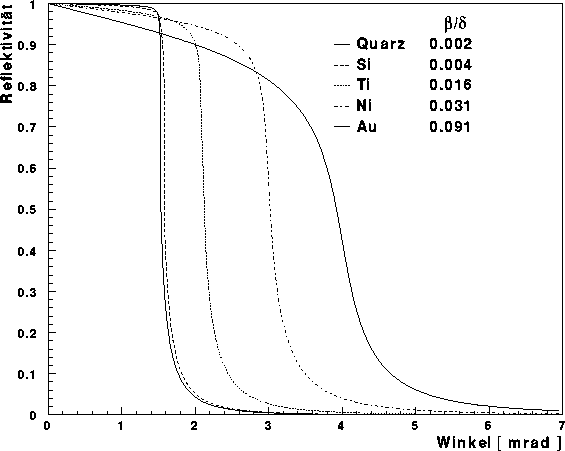
Abbildung: Reflektivität gegen Einfallswinkel - Für verschiedene
Reflektormaterialien ist die Reflektivität gegen den Einfallswinkel
bezüglich einer Energie von 20 keV aufgetragen.
Die Abhängigkeit des kritischen Winkels von der Elektronendichte im
Reflektormaterial ist deutlich zu erkennen. Außerdem hängt der
Kurvenverlauf vom Verhältnis
ab. Je größer die Absorption im Reflektormaterial ist, desto
flacher verläuft die Kurve
Trägt man die Reflektivität gegen die Energie der einfallenden Strahlung
auf, werden die Absorptionseffekte deutlicher. Dies ist in Abbildung
für Silizium und für Gold mit verschiedenen Einfallswinkeln in
einen Energiebereich von 1 bis 30 keV zu sehen. An den Absorptionskanten
nimmt die Reflektivität jeweils abrupt ab und steigt für die höheren
Energien langsam wieder an. Bei Silizium liegt nur die K-Kante mit 1.84 keV
im betrachteten Energiebereich. Bei Gold liegen dahingegen sowohl die M-
(2.21 bis 3.43 keV) als auch die L-Bindungsenergien (11.92 bis
14.35 keV) in diesem Bereich. Dies führt, wie zu erkennen ist, zu einer
Unterdrückung der Reflexion für die Energien oberhalb der
Absorptionskanten.
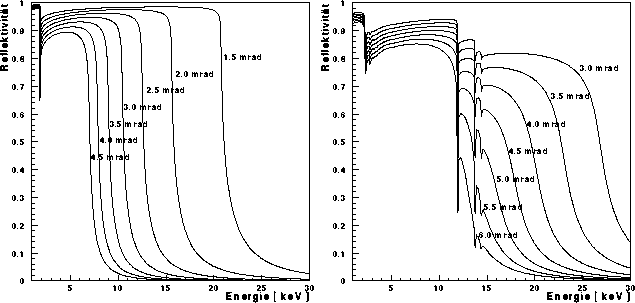
Abbildung: Reflektivität gegen Energie - Für verschiedene Einfallswinkel ist
die Reflektivität gegen die Energie der einfallenden Strahlung einmal für
einen Siliziumwafer und
einmal für einen Goldwafer aufgetragen. An den jeweiligen
Absorptionskanten wird die Reflektivität unterdrückt.
Neben dem aus der Optik stammenden Ansatz über elektromagnetische Wellen und Fresnelformeln kann die Reflexion von Röntgenstrahlung auch aus der Darwin-Prins Theorie hergeleitet werden [Com35]. Hierbei wird die Streuung der Strahlung an Atomlagen betrachtet, die parallel zur Oberfläche zu Schichten zusammengefasst werden. Dieser aus der Kristallographie stammende Ansatz führt zum gleichen Ergebnis [Hen72] [Hen93].
