Eindringtiefe

Gerade bei Oberflächenuntersuchungen ist die Eindringtiefe der Röntgenstrahlung interessant. Unter Eindringtiefe ist hierbei die Tiefe unter der Oberfläche zu verstehen, in der die Intensität des eindringenden Strahls auf 1/e herabgefallen ist. Unter Vernachlässigung der Effekte der Reflexion und Brechunng können zunächst Einfallswinkel betrachtet werden, die deutlich über dem kritischen Winkel liegen. Die Eindringtiefe ergibt sich hiebei mit:

 

Die Eindringtiefe hängt in diesem Fall direkt mit dem Kehrwert des linearen Absorptionskoeffizienten zusammen. Unter Berücksichtigung der Brechung wird der Einfallwinkel in Gleichung durch den Brechungswinkel ersetzt. Für kann dieser näherungsweise mit abgeschätzt werden. Daraus folgt, daß die Brechung erst im Bereich des kritischen Winkels eine Rolle spielt.
Bei Einfallswinkeln unterhalb des kritischen Winkels hat der Wellenvektor im Medium keine reale Komponente senkrecht zur Oberfläche. Dennoch dringt ein Anteil der Strahlung in das Medium ein und wird dort mit zunehmender Tiefe abgeschwächt.
Unter Berücksichtigung der Brechung und Totalreflexion ergibt sich[Par54]:

 

Im Bereich des kritischen Winkels fällt die Eindringtiefe relativ schnell um einen Faktor 10 - 100 ab. Bei kleineren Winkeln geht sie dann gegen einen Grenzwert, der vom Reflektormaterial abhängt. Für ergibt sich:

  
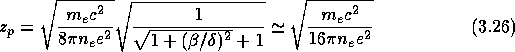
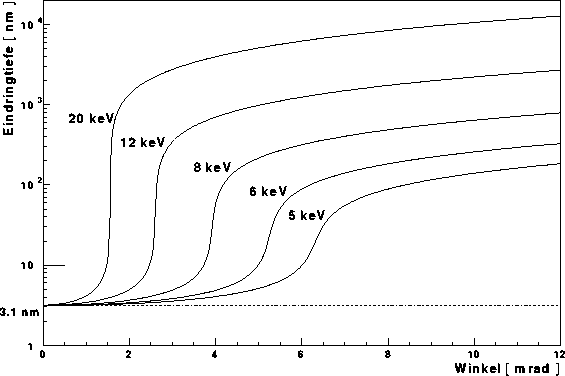
Abbildung: Eindringtiefen für verschiedene Energien - Die Eindringtiefen in eine Siliziumschicht sind für Strahlung unterschiedlicher Energie gegen den Einfallswinkel aufgetragen. Für kleine Einfallswinkel gehen die Kurven alle gegen einen Grenzwert von 3.1 nm.

Der Grenzwert hängt nur über das Verhältnis von der Energie der Strahlung ab. Da dieses Verhältnis jedoch im allgemeinen klein ist (< 0.1, im Bereich außerhalb der Absorptionskanten, siehe Kapitel ), läßt sich näherungsweise sagen, daß die Eindringtiefe für kleine Winkel energieunabhängig ist. Weiterhin ist zu beachten, daß für extrem kleine Winkel die Eindringtiefe größer ist, als es nach zu erwarten wäre, wenn der Strahl nicht gebrochen würde (siehe auch Abbildung ).
In Abbildung ist für eine Siliziumoberfläche die Eindringtiefe gegen den Einfallswinkel aufgetragen. Es ist deutlich zu sehen, wie die Eindringtiefe für verschiedene Energien im Bereich des jeweiligen kritichen Winkels abrupt ansteigt. Bei 20 keV ändert sie sich im Bereich 1.4 bis 1.8 mrad fast um einen Faktor 1000. Bei kleinen Winkeln geht sie allerdings energieunabhängig gegen einen Wert von 3.1 nm. Die Eindringtiefen in verschiedene Reflektoren sind in Abbildung zu sehen. Bezüglich einer Energie von 20 keV sind diese für Silizium, Titan, Nickel und Gold gegen den Einfallswinkel aufgetragen. Der Grenzwert für kleine Winkel nimmt, wie erwartet, mit wachsender Ordnungszahl ab. Für Gold liegt er bei etwa 1.2 nm.

  
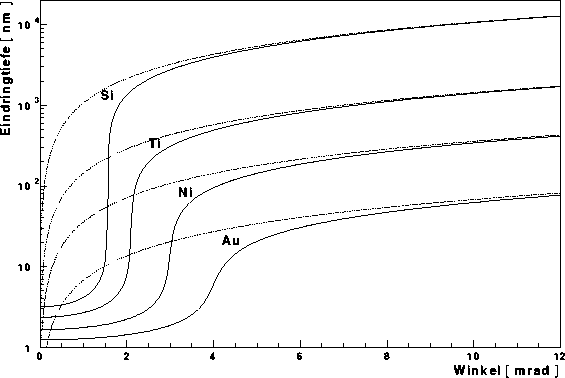
Abbildung: Eindringtiefen in verschiedene Reflektormaterialien - Zu sehen sind hier die Eindringtiefen in unterschiedliche Marterialien für eine Energie von 20 keV. Die gepunkteten Kurven entsprechen hypothetischen Eindringtiefen ohne Totalreflexion an der Oberfläche.

Betrachtet man die absolute Intensität der einfallenden Strahlung, so ist auch die Reflexion zu berücksichtigen. Die Intensität in einer bestimmten Tiefe im Reflektor wird um den Anteil der an der Oberfläche reflektierten Strahlung abgeschwächt. (dazu mehr in Kapitel ).