Detektornachweiswahrscheinlichkeit bei streifendem Einfall

  Die Nachweiswahrscheinlichkeit eines Halbleiterdetektors hängt wesentlich vom Raumwinkel ab, den der Detektorkristall bezüglich der Strahlungsquelle ausfüllt. Dieser ist für einen bezüglich des Detektorradius R großen Abstand d der Kristalloberfläche von der Quelle etwa proportional zu 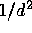. Liegt die Quelle näher am Detektor, so kann der Raumwinkel zum Beispiel nach Gleichung berechnet werden.
Auf dem Weg von der Quelle zum Detektorkristall wird die Strahlung durch verschiedene Absorber abgeschwächt. Üblicherweise schließt ein Berylliumfenster das evakuierte Detektorinnere nach außen ab. Hinzu kommt eine Goldschicht auf dem Kristall und eine Halbleitertotschicht an dessen Oberfläche. Der Hauptteil der zu messenden Strahlung wird allerdings erst in der intrinsischen Schicht des Detektorkristalls absorbiert und dort auch gemessen. Hinzu kommt, wenn auf eine Messung im Vakuum verzichtet wird, die Absorption auf der Luftstrecke zwischen Quelle und Berylliumfenster.
Bei der üblichen Meßgeometrie einer Röntgenfluoreszenzmessung liegt die punktförmig angeregte Stelle auf der Probe mittig vor dem Detektor. Der Raumwinkel läßt sich hierbei wie folgt bestimmen [Deb88]:

 

Bei d >>R geht wie bereits oben erwähnt gegen 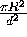. Für diese Geometrie sollte vor quantitativen Messungen eine absolute Efficiencykurve des Detektors in Abhängigkeit von den Energien bestimmt werden (efficiency: engl. für Nachweiswahrscheinlichkeit).
Liegt die Strahlungsquelle nicht mittig vor dem Detektor, hat also eine Ablage von der Mittelachse, so wird zum einen der Abstand größer zum anderen ist die Detektoroberfläche gegenüber der Probe verkippt. Wenn, in einer Ebene im Abstand d parallel zum Detektorkristall, x der Abstand des Strahlflecks von der Detektormittelachse ist, läßt sich Gleichung verallgemeinern:

Dies gilt allerdings nur, solange die Detektoroberfläche nicht durch Blenden oder Kollimatoren abgeschattet wird ( dazu mehr in Kapitel ). Zudem ist hierbei noch die stärkere Absorption auf dem Weg zum Detektorkristall zu berücksichtigen. Zum einen werden die Absorber schräg durchstrahlt und zum anderen wird die Luftstrecke länger.
Bei streifendem Einfall der Strahlung auf das Target kann man nicht mehr von einem punktförmigen Strahlfleck ausgehen. Der Strahlfleck wird proportional zu 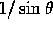gestreckt (siehe Abbildung ). Die anregende Intensität pro Fläche auf dem Target nimmt mit der Länge dieses Strahlflecks ab. Die Intensität, die durch den Detektor gemessen wird, ist proportional zu einem Integral über die Länge des Strahlflecks:

D(x) soll hierbei 1 sein, wenn an der Stelle x eine Anregung stattfinden kann, und 0, wenn dies nicht der Fall ist, da sich zum Beispiel dort gar kein Probenmaterial befindet. Nimmt man eine Gleichverteilung der anregenden Intensität I(x) über die Strahlbreite b an und geht davon aus, daß die Mitte des Strahlflecks vor dem Detektor liegt, ergibt sich:

Für kleine Winkel geht das Integral gegen einen Grenzwert. Da zum einen der Öffnungswinkel des Detektors begrenzt und zum anderen die Probe nicht unendlich ausgedehnt ist, tragen die äußeren Bereiche des Strahlflecks nichts mehr bei. Man kann näherungsweise davon ausgehen, daß die anregende Intensität für kleine Winkel proportional zu ist.

  
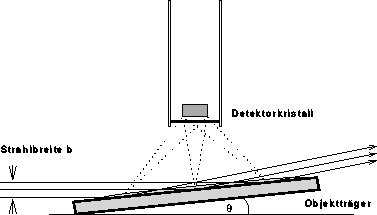
Abbildung: Raumwinkel des Detektors - Bei streifendem Einfall auf eine Probe zieht sich der Strahlfleck proportional zu 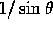in die Länge. Die Anregung findet nicht mehr direkt vor dem Detektor statt und der Raumwinkelanteil, den der Detektorkristall bezüglich der Probe ausfüllt, verkleinert sich. Bei extremer Ausdehnung des Strahlflecks liegt die Anregung teilweise außerhalb des Öffnungswinkels des Detektors.