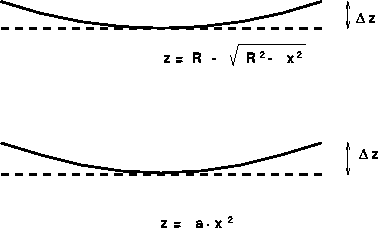Next: Messungen mit Totalreflexion
Up: Röntgentotalreflexion
Previous: Detektornachweiswahrscheinlichkeit bei streifendem
Einfall
Im folgenden Abschnitt werden einige Effekte genannt, die bei realen
Strahlverhältnissen und Reflektoroberflächen die Reflexion
beeinträchtigen. Zunächst werden hierbei Unregelmäßigkeiten der
Oberfläche betrachtet. Dabei kann grundsätzlich zwischen drei Effekten
unterschieden werden [San92][ZEI92]: Oberflächenrauhigkeit,
Welligkeit (engl.: waviness) und Formfehler. Der Unterschied liegt im
wesentlichen in der Größenordnung der Abweichung und der Ortsfrequenz, mit
der sich die Unregelmäßigkeit über die Oberfläche verteilt.
Die Rauhigkeit unterscheidet sich zudem durch ihre zufällige Verteilung von den anderen beiden Effekten. Sie führt daher zu einer zusätzlichen Streuung des zu reflektierenden Strahls.
Sie liegt im Regelfall, natürlich abhängig von der Oberflächenbehandlung, in der Größenordnung einiger Ångstrom.
Unter Welligkeit ist dahingegen eine periodische Unregelmäßigkeit der
Oberfläche zu verstehen, deren Ursprung meist im Polieren des Reflektors
liegt. Die Periode kann in der Größenordnung Mikrometer bis Millimeter
liegen. Hieraus ergibt sich eine Defokussierung des reflektierten Strahls. Die
größenordnungsmäßig extremsten Abweichungen ergeben sich durch
Formfehler. Hierbei weicht die Reflektoroberfläche im ganzen von ihrer
Sollform ab. Dies kann zum einen durch fehlerhafte Herstellung bedingt
sein. Zum anderen kann sich der Reflektor später durch thermische Ausdehnung
oder mechanische Belastung verformen. Auch hierdurch ergibt sich eine
Defokussierung des Strahls. Der reflektierte Strahl weicht teilweise von der
erwarteten Reflexionsrichtung ab. In dieser Arbeit werden aber in erster Linie
die Änderungen der Reflektivität durch die Oberflächenunregelmäßigkeiten
abgeschätzt.
Anschließend werden die Auswirkungen der Strahldivergenz auf die Reflexion
betrachtet. Dabei ist zu bedenken, daß jede Reflexion eines divergenten
Strahls diesen zusätzlich aufweitet.
Trifft ein divergenter Strahl auf den Reflektor, so muß man zudem einen
ganzen Bereich von Einfallswinkeln betrachten, die jeweils andere
Reflektivitäten ergeben. Hiernach wird noch einmal die Strahlaufweitung durch
Streuung betrachtet.
Bei der korrekten Berechnung der Reflexion an einer Oberfläche ist deren
Rauhigkeit zu berücksichtigen. Eine rauhe Oberfläche führt zu einer
zusätzlichen Streuung der einfallenden Strahlung. Der Strahl wird hierdurch
aufgeweitet [SHA94].
Das Rauhheitsprofil einer Oberfläche kann durch verschiedene Größen
charakterisiert werden (DIN 4762, DIN 4768, [HER95]). Die maximale
Rauhtiefe 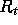 ist der Abstand zwischen dem höchsten und dem tiefsten Punkt
des Rauhheitsprofil. Die Glättungstiefe
ist der Abstand zwischen dem höchsten und dem tiefsten Punkt
des Rauhheitsprofil. Die Glättungstiefe 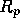 ist der Abstand zwischen dem
höchsten Punkt und der Mittellinie des Rauhheitsprofils. Der Mittenrauhwert
ist der Abstand zwischen dem
höchsten Punkt und der Mittellinie des Rauhheitsprofils. Der Mittenrauhwert
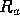 ist der arithmetische Mittelwert aller Abstände R des Rauheitsprofils
von dessen Mittellinie. Bei theoretischen Betrachtungen der
Oberflächenrauhigkeit wird üblicherweise der quadratische Mittelwert
ist der arithmetische Mittelwert aller Abstände R des Rauheitsprofils
von dessen Mittellinie. Bei theoretischen Betrachtungen der
Oberflächenrauhigkeit wird üblicherweise der quadratische Mittelwert
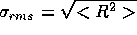 betrachtet. Dieser wird auch als 'rms roughness'
bezeichnet (rms: root mean square) [ZEI92][Nev80].
betrachtet. Dieser wird auch als 'rms roughness'
bezeichnet (rms: root mean square) [ZEI92][Nev80].
Ist die Oberflächenrauhigkeit nicht zu groß im Vergleich zu den betrachteten
Wellenlängen, so kann die Oberfläche als mehrschichtiger Reflektor
betrachtet werden. Man teilt sie in übereinanderliegende Schichten ein, denen
mit zunehmender Tiefe höhere Dichten zugeordnet werden. Der Brechungsindex
einer einzelnen Schicht n ergibt sich mit 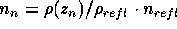 aus dem Brechungsindex des Reflektormaterials und dem Verhältnis
der zugeordneten Dichte zur Dichte des Reflektormaterials.
Beim einfachsten Modell entspricht das Rauhheitsprofil der Oberfläche einer
linearen Dichtezunahme bis zur Tiefe
aus dem Brechungsindex des Reflektormaterials und dem Verhältnis
der zugeordneten Dichte zur Dichte des Reflektormaterials.
Beim einfachsten Modell entspricht das Rauhheitsprofil der Oberfläche einer
linearen Dichtezunahme bis zur Tiefe 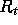 [Schw92]:
[Schw92]:
Allerdings ist eher eine statistische Normalverteilung des Tiefenprofils um
die mittlere Tiefe zu erwarten. Somit ergibt sich in einem weitergehenden
Modell folgende Dichteverteilung [Nev80][SHA94]:
Die Gesamtreflexion eines solchen Schichtsystems läßt sich mit der in
Kapitel  beschriebenen Rekursionsformel berechnen.
beschriebenen Rekursionsformel berechnen.
Nevot und Croce haben gezeigt, daß sich mit einer angenommenen
Normalverteilung des Dichteprofils folgender Faktor für das Verhältnis der
Reflektivitäten eines rauhen Reflektors und eines idealen Reflektors ergeben
[Nev80]:
In Abbildung  ist die Reflektivität eines Siliziumreflektors bei
einem Einfallswinkel von 2 mrad gegen die einfallende Energie
aufgetragen. Hierbei wurden mit Hilfe des Nevot Croce Faktors die
Reflektivitäten bei verschiedenen Oberflächenrauhigkeiten berechnet. Bei
zunehmender Rauhigkeit wird die Gesamtreflektivität abgeschwächt. Die
stärkste Abschwächung ist hierbei für die Energien zu beobachten, deren
kritischer Winkel unterhalb des Einfallswinkels liegt.
ist die Reflektivität eines Siliziumreflektors bei
einem Einfallswinkel von 2 mrad gegen die einfallende Energie
aufgetragen. Hierbei wurden mit Hilfe des Nevot Croce Faktors die
Reflektivitäten bei verschiedenen Oberflächenrauhigkeiten berechnet. Bei
zunehmender Rauhigkeit wird die Gesamtreflektivität abgeschwächt. Die
stärkste Abschwächung ist hierbei für die Energien zu beobachten, deren
kritischer Winkel unterhalb des Einfallswinkels liegt.
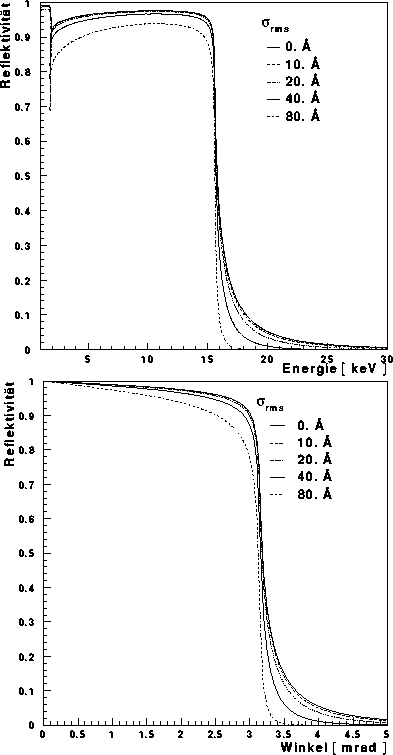
Abbildung: Reflektivität einer rauhen Siliziumoberfläche - Im oberen Bild
wurde ein
Einfallwinkel von 2 mrad betrachtet und die Reflektivität für
unterschiedliche Rauhigkeiten gegen die
Energie der einfallende Strahlung aufgetragen. Im unteren Bild wurden die
Reflektivitätskurven für eine Energie von 10 keV gegen den
Einfallswinkel aufgetragen
Trägt man die Reflektivität für eine bestimmte Energie gegen den
Einfallswinkel auf, so sieht man, daß gerade im Bereich des kritischen
Winkels die Intensität der reflektierten Strahlung abgeschwächt wird.
Die Welligkeit eines Reflektors führt zu lokalen Änderungen bei der Neigung der Oberfläche.
Betrachtet man ein Profil z(y) entlang der Oberfläche in Strahlrichtung, so
läßt sich ein Neigungsfehler (engl. slope error) definieren. Dies ist im
allgemeinen der quadratische Mittelwert der Abweichungen von der mittleren
Neigung 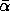 [San92]:
[San92]:
Da die Perioden der Welligkeit viel größer sind als die Wellenlängen der
reflektierten Strahlung, ist der Reflektor lokal als plan zu betrachten. Die
Welligkeit äußert sich durch Reflexionswinkel, die von der
Hauptreflexionsrichtung abweichen. Wenn  der erwartete
Reflexionswinkel für eine ideale Reflektoroberfläche ist, ergibt sich bei
einer lokal abweichenden Neigung
der erwartete
Reflexionswinkel für eine ideale Reflektoroberfläche ist, ergibt sich bei
einer lokal abweichenden Neigung 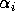 der tatsächliche Reflexionswinkel
mit:
der tatsächliche Reflexionswinkel
mit:
In einem einfachen Modell kann die Welligkeit berücksichtigt werden, indem
man die Form der Reflektoroberfläche als Sinuskurve betrachtet, deren
Wellenlänge der Länge des Reflektors L entspricht und die den
Neigungsfehler 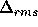 aufweist. Die Amplitude A der Sinuskurve ergibt sich aus:
aufweist. Die Amplitude A der Sinuskurve ergibt sich aus:
Ein Verfahren zur Berechnung der Strahloptik bei Neigungsfehlern, das sich an
der realen Oberflächenstruktur orientiert, wird im Programm SHADOW verwendet
[SHA94][San92].
Hierbei geht man vom realen Profil der Reflektoroberfläche aus. Nach einer
Fouriertransformation des Profils wird die Reflexion an den Sinusgittern
berechnet, die den Hauptortsfrequenzen entsprechen.
Da die Welligkeit in erster Linie die Strahloptik spezifisch beeinträchtigt,
wurde sie
im Rahmen dieser Arbeit nicht weiter betrachtet. Ihr Einfluß auf die
Reflektivität ist eher genereller Natur und kann genausogut über Formfehler
bzw. Divergenz berücksichtigt werden.
Um einen Fehler bei der Form des Reflekors korrekt berücksichtigen zu
können, muß ein Profil der Oberfläche aufgenommen werden. Dies kann mittels
Laserinterferometrie geschehen oder durch Abtasten der Oberfläche
[ZEI92]. Das Interesse liegt hierbei auf den Abweichungen von der
Sollform, die in der Größenordnung jenseits von Rauhigkeit und Welligkeit
liegen. Mit der realen Form des Reflektors, die man aus dem Profil erhält,
kann hiernach die Reflexion berechnet werden.
Die Sollform im vorliegenden Fall soll eine plane Oberfläche sein. Wie
bereits erwähnt liegt das Interesse auf Abweichungen bei der Reflektivität
und weniger auf der Berechnung der Strahloptik. Daher soll am Beispiel zweier
Formfehler, die zum Beispiel durch mechanische Belastung des Reflektors
entstanden sein könnten, der Einfluß auf die Reflektivität abgeschätzt
werden (siehe Abbildung  ).
).
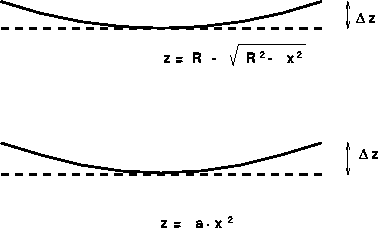
Abbildung: Formfehler einer planen Reflektoroberfläche
Dazu wird der maximale Neigungsfehler betrachtet, der sich durch
mögliche Abweichungen 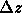 von der Sollform ergibt.
Zum einen wird eine kreisförmige Verformung angenommen:
von der Sollform ergibt.
Zum einen wird eine kreisförmige Verformung angenommen:
und zum anderen eine Parabelform:
Geht man von einem Spiegel von 100 mm Länge aus, so würde ein maximaler
Neigungsfehler von 0.5 mrad bei
Gleichung  einer Profilabweichung von
einer Profilabweichung von 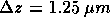 an den Kanten entsprechen. Für die parabelförmige Abweichung ergibt sich
dementsprechend
an den Kanten entsprechen. Für die parabelförmige Abweichung ergibt sich
dementsprechend 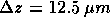 .
.
Die beschriebenen Formfehler können bei ihren Auswirkungen auf die
Reflektivität als zusätzliche Divergenz des Strahls betrachtet werden.
In beiden Fällen handelt es sich um Abweichungen vom Einfallswinkel,
die in ihren Auswirkungen auf den weiteren Strahlverlauf grundsätzlich nicht
unterschieden werden können.
Wie bereits in Kapitel 1 gezeigt, ist auch bei Synchrotronstrahlung noch mit
einer endlichen Strahldivergenz zu rechnen.
Bei der Reflexion eines divergenten Strahls ist zu beachten, daß der
Ablenkungswinkel des Strahls dem doppelten des Einfallswinkels auf die
reflektierende Oberfläche entspricht.
Die Divergenz der Strahlung verdoppelt sich sozusagen. Das ist vor allem im
Hinblick auf Mehrfachreflexionen zu berücksichtigen.
Unter Berücksichtigung der Divergenz der einfallenden Strahlung ergibt sich
die Reflektivität für einen Einfallswinkel 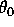 aus dem Intergal der
Reflektivitäten über die gesamte Winkelverteilung:
aus dem Intergal der
Reflektivitäten über die gesamte Winkelverteilung:
Hierbei soll 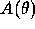 die winkelabhängige Intensitätsverteilung sein, deren Integral über den gesamten Winkelbereich auf eins normiert ist.
Im einfachsten Fall einer Gleichverteilung über den Winkelbereich von
die winkelabhängige Intensitätsverteilung sein, deren Integral über den gesamten Winkelbereich auf eins normiert ist.
Im einfachsten Fall einer Gleichverteilung über den Winkelbereich von 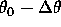 bis
bis 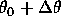 folgt hieraus:
folgt hieraus:
Eine solche Verteilung entspricht der erwarteten horizontalen Verteilung der
Synchrotronstrahlung bei idealen Elektronenstrahlbedingungen. In Abbildung
 sind die berechneten Reflektivitäten an einem Siliziumreflektor
bei 2 mrad zu sehen unter der Berücksichtigung verschiedener Divergenzen
sind die berechneten Reflektivitäten an einem Siliziumreflektor
bei 2 mrad zu sehen unter der Berücksichtigung verschiedener Divergenzen
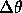 . Hierbei wird der Kurvenverlauf um die Energie, bei der
erstmals Totalreflexion auftritt, abgeflacht.
. Hierbei wird der Kurvenverlauf um die Energie, bei der
erstmals Totalreflexion auftritt, abgeflacht.
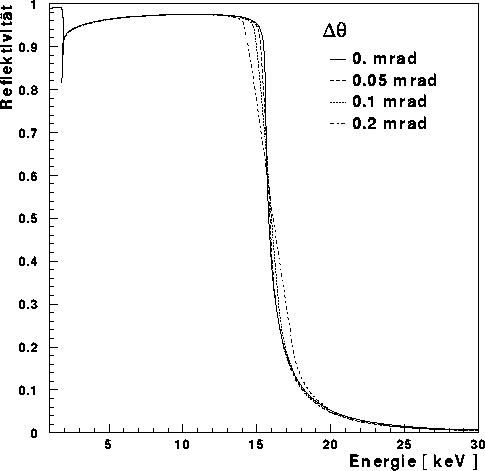
Abbildung: Reflektivität bei divergentem Strahl - Die Reflektivität an einer
Siliziumoberfläche unter 2 mrad ist für verschiedene Strahldivergenzen
gegen die Energie der einfallenden Strahlung aufgetragen.




Next: Messungen mit Totalreflexion
Up: Röntgentotalreflexion
Previous: Detektornachweiswahrscheinlichkeit bei streifendem
Einfall
Anno Hein
Fri Apr 4 12:36:40 CEST 1997