



Next: TXRF mit Objektträger
Up: Messungen mit Totalreflexion
Previous: Röntgenspiegel - 'high energy
Mit Hilfe der Winkelabhängigkeit der Eindringtiefe bei streifendem Einfall
wurden an einem dreischichtigen Target schichtenaufgelöste
Fluoreszenzmessungen durchgeführt. Es handelte sich dabei um einen
beschichteten Siliziumwafer (Durchmesser 100 mm). Auf der
Siliziumoberfläche lag eine Chromschicht und darauf eine Goldschicht. Die
Dicken
der beiden oberen Schichten sollten jeweils im Bereich 5 bis 50 nm
liegen [Pan94]. Eine SYXRF Analyse des Wafers ergab eine Dicke der
Goldschicht von etwa 10 nm und der Chromschicht von etwa 20 nm.
Eine programminterne Steuerung des Goniometers ist zur Zeit noch nicht
möglich. Daher wurde der Winkel zu jeder Messung einzeln eingestellt. Die
Meßdauer war jeweils 300 s.
Die ersten Messungen bei streifendem Einfall wurden zunächst ohne Kollimator
durchgeführt. Um eine ausreichende Anregung der Silizium K-Schale
( 1.839 keV) zu ereichen, wurde ein Aluminiumabsorber von 0.7 mm
gewählt. Dies
führte teilweise zu recht hohen Fluoreszenzintensitäten, so daß der Detektor
in eine relativ weite Position zurückgefahren werden mußte ( 9 bis 10 mm
vom Strahl entfernt). Dadurch ergaben sich zu hohe Si- und Ti-Raten
für
kleine Winkel, da Anregungen und Streuungen an der Vorderkante des Wafers im
Öffnungswinkel des Detektors lagen. Der Öffnungswinkel wurde daher bei den
späteren Messungen durch Kollimatoren auf den
unmittelbaren Bereich vor dem Detektor beschränkt.
In Abbildung  sind die aufgenommenen relativen
Fluoreszenzintensitäten für Silizium, Chrom und Gold zu sehen. Die Messungen
wurden jeweils mit einem der beiden Kollimatoren (vgl. Kap
sind die aufgenommenen relativen
Fluoreszenzintensitäten für Silizium, Chrom und Gold zu sehen. Die Messungen
wurden jeweils mit einem der beiden Kollimatoren (vgl. Kap  )
durchgeführt (links: 10 mm Innendurchmesser, rechts: 8 mm Innendurchmesser). Zudem stand der Fluoreszenzdetektor bei der ersten Messung
(links) in einer näheren Position zum Target. Wie deutlich zu sehen ist,
konnte so die Fluoreszenzstrahlung des Siliziums im Gegensatz zur zweiten
Messung mit einer akzeptablen Zählrate aufgenommen werden. Allerdings hatte
dies zur Folge, daß die aufgenommene Goldfluoreszenzintensität eventuell
aufgrund der Detektortotzeit teilweise unterdrückt wurde.
Bei der zweiten Messung ist ein ausgeprägtes Maximum der Goldfluoreszenz bei
einem Winkel von etwa 5 bis 6 mrad zu erkennen. Das Maximum ist bei der
ersten
Messung zwar auch zu erkennen, aber es ist anscheinend durch die genannten
Totzeiteffekte unterdrückt.
)
durchgeführt (links: 10 mm Innendurchmesser, rechts: 8 mm Innendurchmesser). Zudem stand der Fluoreszenzdetektor bei der ersten Messung
(links) in einer näheren Position zum Target. Wie deutlich zu sehen ist,
konnte so die Fluoreszenzstrahlung des Siliziums im Gegensatz zur zweiten
Messung mit einer akzeptablen Zählrate aufgenommen werden. Allerdings hatte
dies zur Folge, daß die aufgenommene Goldfluoreszenzintensität eventuell
aufgrund der Detektortotzeit teilweise unterdrückt wurde.
Bei der zweiten Messung ist ein ausgeprägtes Maximum der Goldfluoreszenz bei
einem Winkel von etwa 5 bis 6 mrad zu erkennen. Das Maximum ist bei der
ersten
Messung zwar auch zu erkennen, aber es ist anscheinend durch die genannten
Totzeiteffekte unterdrückt.
Die einzelnen Fluoreszenzspektren wurden anhand der aufgenommenen
Streuspektren aufeinander normiert. Der abgeschätzte Fehler liegt für die
Normierung bei
5 %. Der Winkel wurde mit dem beschriebenen Goniometer
eingestellt. So kann der relative Fehler mit <0.1 mrad angenommen
werden, was etwa einem Schritt des Schrittmotors entsprechen würde. Hinzu
kommt ein absoluter Fehler, da die Nullstellung der Reflexion nur
schwer zu bestimmen ist. Hierdurch verschieben sich die Kurven
allerdings nur entlang der Abzisse. Problematisch war die Bestimmung
der Strahlbreite, die über die
Detektorgeometrie die meßbare Intensität beeinflußt (siehe Kapitel
 ). Bei der ersten
Messung war eine horizontale Blende von 200
). Bei der ersten
Messung war eine horizontale Blende von 200 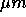 Breite eingestellt und bei
der zweiten eine Blende von 300
Breite eingestellt und bei
der zweiten eine Blende von 300 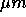 .
.
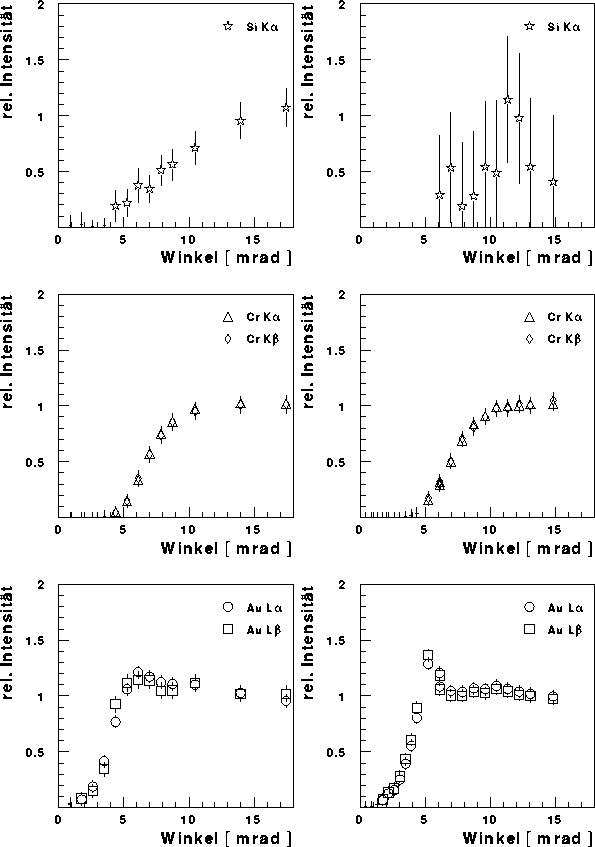
Abbildung: Relative Fluoreszenzintensitäten einer dreischichtigen Probe - Zu
sehen sind hier die gemessenen relativen Fluoreszenzintensitäten der
Siliziumbasisschicht und der beiden aufliegenden Schichten aus Chrom
und Gold. Die Messungen links und rechts wurden jeweils mit unterschiedlichen
Kollimatoren durchgeführt (siehe Beschreibung im Text). Die
einzelnen Fluoreszenzspektren sind anhand der Streumessungen
gegeneinander normiert worden.
Die relative Intensität der Au 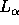 - und Au
- und Au 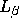 -
Linie speziell bei der zweiten Messung ließ eine Abschätzung der
Schichtdicke des Goldes zu. Hierzu wurden auf Grundlage der Gleichung
-
Linie speziell bei der zweiten Messung ließ eine Abschätzung der
Schichtdicke des Goldes zu. Hierzu wurden auf Grundlage der Gleichung
 die theoretischen relativen Fluoreszenzintensitäten für
verschiedene Schichtdicken berechnet. In Abbildung
die theoretischen relativen Fluoreszenzintensitäten für
verschiedene Schichtdicken berechnet. In Abbildung  ist eine
Beispielrechnung für unterschiedlich dicke Kobaltschichten auf einer
Siliziumoberfläche zu sehen. Für eine monochromatische Anregung von
17.44 keV wurde die jeweilige relative Intensität der Co
ist eine
Beispielrechnung für unterschiedlich dicke Kobaltschichten auf einer
Siliziumoberfläche zu sehen. Für eine monochromatische Anregung von
17.44 keV wurde die jeweilige relative Intensität der Co 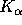 -Linie
berechnet. Die Ergebnisse wurden mit veröffentlichten Berechnungen anderer
Arbeitsgruppen verglichen [dBoe91] [Schw92].
-Linie
berechnet. Die Ergebnisse wurden mit veröffentlichten Berechnungen anderer
Arbeitsgruppen verglichen [dBoe91] [Schw92].
Um eine polychromatische Anregung zu
berücksichtigen, mußten die Fluoreszenzwahrscheinlichkeiten über das
anregende
Spektrum integriert werden. Mit Hilfe tabellierter
Ionisationsquerschnitte der AuL-Schalen, der Wahrscheinlichkeiten für
Coster-Kronig Übergänge und der Wahrscheinlichkeiten der
einzelnen Fluoreszenzübergänge [Sco73] [Kra78] konnten die relativen
Fluoreszenzintensitäten der 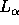 - und
- und 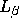 -
Strahlung für einzelne anregende Energien berechnet werden. Die anregende
spektrale Verteilung, die zur Berechnung benutzt wurde, entsprach einem
Elektronenstrom von 2.3 GeV und einem Aluminiumabsorber von 0.7 mm.
Nach Gleichung
-
Strahlung für einzelne anregende Energien berechnet werden. Die anregende
spektrale Verteilung, die zur Berechnung benutzt wurde, entsprach einem
Elektronenstrom von 2.3 GeV und einem Aluminiumabsorber von 0.7 mm.
Nach Gleichung  wurde die Detektorgeometrie berücksichtigt.
Die Absorption der Fluoreszenzstrahlung wurde vernachlässigt, da sie zum
einen aufgrund der dünnen Schicht klein ist und da sich zum
anderen der Winkel der Targetoberfläche zur Detektormittelachse kaum
ändert.
wurde die Detektorgeometrie berücksichtigt.
Die Absorption der Fluoreszenzstrahlung wurde vernachlässigt, da sie zum
einen aufgrund der dünnen Schicht klein ist und da sich zum
anderen der Winkel der Targetoberfläche zur Detektormittelachse kaum
ändert.
In Abbildung  sind die
theoretischen Fluoreszenzintensitäten der Au
sind die
theoretischen Fluoreszenzintensitäten der Au 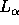 - und
Au
- und
Au 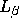 -Linie gegen den Einfallwinkel aufgetragen. Dabei wurde
eine Chromschicht von 20 nmund Goldschichten von 6, 7, 8
bzw. 10 nm angenommen. Eingezeichnet sind zudem die entsprechenden
gemessenen Fluoreszenzintensitäten, wobei der Winkel allerdings um
-0.3 mrad korrigiert werden mußte. Der Kollimator, der bei der
Messung benutzt und bei der Rechnung berücksichtigt wurde, hatte einen
Innendurchmesser von
8 mm und eine Länge von 18 mm. Der Targetpunkt lag
hierbei in einem Abstand von 90 mm zum Detektorkristall.
Um die theoretischen Kurven an
die experimentellen Werte anzupassen, mußte eine Strahlbreite von
-Linie gegen den Einfallwinkel aufgetragen. Dabei wurde
eine Chromschicht von 20 nmund Goldschichten von 6, 7, 8
bzw. 10 nm angenommen. Eingezeichnet sind zudem die entsprechenden
gemessenen Fluoreszenzintensitäten, wobei der Winkel allerdings um
-0.3 mrad korrigiert werden mußte. Der Kollimator, der bei der
Messung benutzt und bei der Rechnung berücksichtigt wurde, hatte einen
Innendurchmesser von
8 mm und eine Länge von 18 mm. Der Targetpunkt lag
hierbei in einem Abstand von 90 mm zum Detektorkristall.
Um die theoretischen Kurven an
die experimentellen Werte anzupassen, mußte eine Strahlbreite von
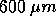 am Targetpunkt angenommen werden. Die Divergenz des
Strahls wurde bei den Berechnungen nicht berücksichtigt. Sie würde
den Kurvenverlauf allerdings nur geringfügig verwischen.
am Targetpunkt angenommen werden. Die Divergenz des
Strahls wurde bei den Berechnungen nicht berücksichtigt. Sie würde
den Kurvenverlauf allerdings nur geringfügig verwischen.
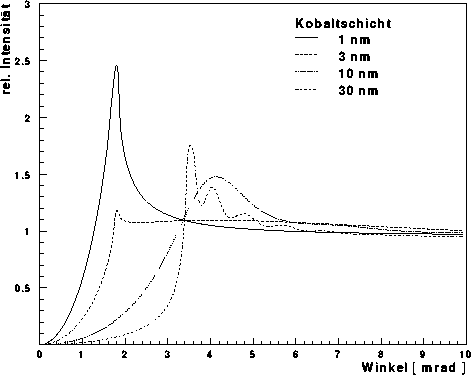
Abbildung: Theoretische relative Fluoreszenzintensität einer Kobaltschicht auf
Silizium - Zum Test des Programms wurden für eine monochromatische Anregung
von 17.44 keV (Mo 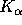 ) die Fluoreszenzintensitäten
unterschiedlich dicker Kobaltschichten auf einer Siliziumoberfläche
berechnet.
Zu sehen sind die theoretischen relativen Fluoreszenzintensitäten
der Co
) die Fluoreszenzintensitäten
unterschiedlich dicker Kobaltschichten auf einer Siliziumoberfläche
berechnet.
Zu sehen sind die theoretischen relativen Fluoreszenzintensitäten
der Co  -Linie bei Schichtdicken von 1, 3, 10 und
30 nm. Die Fluoreszenzanregung an sich ist hierbei der Übersicht halber
auf 1 normiert, d.h. alle Kurven laufen auf ein Plateau von 1
hinaus. Tatsächlich wächst die Fluoreszenzintensität insgesamt mit der
Schichtdicke (siehe Abbildung
-Linie bei Schichtdicken von 1, 3, 10 und
30 nm. Die Fluoreszenzanregung an sich ist hierbei der Übersicht halber
auf 1 normiert, d.h. alle Kurven laufen auf ein Plateau von 1
hinaus. Tatsächlich wächst die Fluoreszenzintensität insgesamt mit der
Schichtdicke (siehe Abbildung  ). Bei den kleinen Schichtdicken
ist deutlich die Reflexion an der Siliziumschicht zu erkennen. Die
Co
). Bei den kleinen Schichtdicken
ist deutlich die Reflexion an der Siliziumschicht zu erkennen. Die
Co  -Linie durchläuft beim kritischen Winkel für Silizium
(1.8 mrad) ein Maximum. Die Reflexion an der Kobaltschicht ist aufgrund
von Interferenz unterdrückt. Bei größeren Schichtdicken ist die Reflexion
an der Kobaltschicht allerdings entscheidend. Der kritische Winkel liegt bei
3.6 mrad. Die Anregung ist dort maximal, da zum einen die Transmission in
die Kobaltschicht ansteigt und zum anderen der Einfallswinkel
extrem flach ist. Die Nebenmaxima und -minima entsprechen der schwankenden
Reflektivität des Gesamtsystems. Ist diese niedrig so dringt mehr anregende
Strahlung in die obere Schicht ein und umgekehrt.
Die Kurven stimmen mit von anderen Arbeitsgruppen
veröffentlichten Berechnungen überein [dBoe91] [Schw92].
-Linie durchläuft beim kritischen Winkel für Silizium
(1.8 mrad) ein Maximum. Die Reflexion an der Kobaltschicht ist aufgrund
von Interferenz unterdrückt. Bei größeren Schichtdicken ist die Reflexion
an der Kobaltschicht allerdings entscheidend. Der kritische Winkel liegt bei
3.6 mrad. Die Anregung ist dort maximal, da zum einen die Transmission in
die Kobaltschicht ansteigt und zum anderen der Einfallswinkel
extrem flach ist. Die Nebenmaxima und -minima entsprechen der schwankenden
Reflektivität des Gesamtsystems. Ist diese niedrig so dringt mehr anregende
Strahlung in die obere Schicht ein und umgekehrt.
Die Kurven stimmen mit von anderen Arbeitsgruppen
veröffentlichten Berechnungen überein [dBoe91] [Schw92].
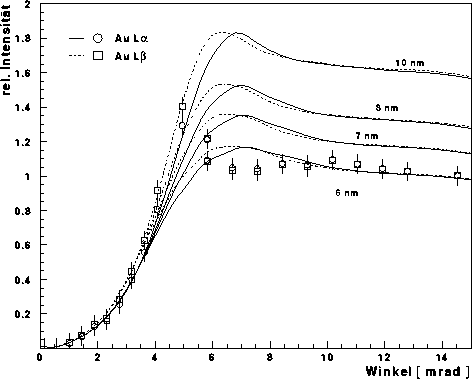
Abbildung: Relative Fluoreszenzintensitäten der Gold L Linien - Zu
sehen sind zum einen die relativen Fluoreszenzintensitäten
der Au 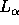 - und Au
- und Au 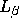 -Linie aus der zweiten Messung
und zum anderen gerechnete
Kurven für eine Chromschicht von 20 nm und Goldschichten von 6, 7,
8 bzw. 10 nm. Die angenommene Strahlbreite liegt bei 600 nm und
als Kollimator wurde der Kollimator 2 (8 mm Innendurchmesser)
berücksichtigt. Im Gegensatz zu Abbildung
-Linie aus der zweiten Messung
und zum anderen gerechnete
Kurven für eine Chromschicht von 20 nm und Goldschichten von 6, 7,
8 bzw. 10 nm. Die angenommene Strahlbreite liegt bei 600 nm und
als Kollimator wurde der Kollimator 2 (8 mm Innendurchmesser)
berücksichtigt. Im Gegensatz zu Abbildung  wurde die
Schichtdicke bei der Fluoreszenzintensität berücksichtigt, so daß die
Höhen der Plateaus für die größeren Winkel im Verhältnis der
Schichtdicken zueinader verschoben sind.
wurde die
Schichtdicke bei der Fluoreszenzintensität berücksichtigt, so daß die
Höhen der Plateaus für die größeren Winkel im Verhältnis der
Schichtdicken zueinader verschoben sind.
Die Kurven haben für kleine Winkel einen in etwa gleichen Verlauf, da die
Schichtdicke dort wegen der geringen Eindringtiefe kaum eine Rolle spielt.
Die Intensität steigt zunächst
aufgrund des Targetwinkels (siehe Kapitel  ) und des
wachsenden Anteils der eindringenden Strahlung an. Da der eindringende
Strahl gebrochen wird, ist die Strecke durch die Schicht
länger.
Bei größeren Einfallswinkeln, die zudem nicht mehr
so stark gebrochen werden, nimmt die Strecke durch die Schicht und
somit auch die Fluoreszenzintensität ab. Die Nebenmaxima und -minima in den
Kurven sind mit der Reflektivität des Gesamtsystems zu erklären. Ist diese
klein so dringt mehr Strahlung in die Goldschicht ein.
Für größere Winkel laufen die Kurven jeweils auf ein Plateau hinaus. Die
relativen Höhen der Plateaus entsprechen den unterschiedlichen
Goldschichtdicken.
) und des
wachsenden Anteils der eindringenden Strahlung an. Da der eindringende
Strahl gebrochen wird, ist die Strecke durch die Schicht
länger.
Bei größeren Einfallswinkeln, die zudem nicht mehr
so stark gebrochen werden, nimmt die Strecke durch die Schicht und
somit auch die Fluoreszenzintensität ab. Die Nebenmaxima und -minima in den
Kurven sind mit der Reflektivität des Gesamtsystems zu erklären. Ist diese
klein so dringt mehr Strahlung in die Goldschicht ein.
Für größere Winkel laufen die Kurven jeweils auf ein Plateau hinaus. Die
relativen Höhen der Plateaus entsprechen den unterschiedlichen
Goldschichtdicken.
Die exerimentellen Werte wurden im vorderen Bereich der Kurven an deren Höhe
angepaßt. Im Gesamtverlauf der Kurven scheinen die Werte am ehesten einer
Schichtdicke zwischen 6 und 7 nm zu entsprechen.
Im vorderen Teil
scheinen sie allerdings eher auf der Kurve für die 10 nm Goldschicht zu
liegen. Allerdings stimmen die experimentelle Werte gerade im Bereich des
Maximums der theoretischen Kurven nicht mit diesen überein. Das Maximum der
experimentellen Werte liegt etwa bei 5 mrad und das der theoretischen
Kurven etwa bei 6 mrad.
Gerade im Bereich 6 bis 9 mrad liegen die experimentellen
Werte etwas zu niedrig. Das kann daran liegen, daß dort bei
relativ hohen Elektronenströmen gemessen wurde. Eine doppelte Messung bei
6 mrad scheint darauf hinzuweisen, daß die gemessene relative Intensität
von der Höhe des Elektronenstroms abhängt. Die erste Messung fand bei
15 mA statt und liegt mit ihrer relativen Intensität etwa 15% über der
Messung bei 70 mA.
Aus Messungen von vertikalen
Strahlprofilen während eines Meßzyklus ist bekannt, daß sich die vertikale
Elektronenstrahlbreite mit der Höhe des Elektronenstroms
ändert. Nimmt man dies auch für die horizontale Elektronenverteilung
an, so würde dies eine größere Elektronenstrahlbreite zur Folge
haben, was die zu geringe Intensität erklären kann.
Ein Fehler bei der Winkeleinstellung, mit dem die Abweichungen zu erklärt
werden könnten, ist nahezu auszuschließen. Dazu müßte das Goniometer
zwischen den einzelnen Messungen jeweils etwa ein bis zwei Schritte zuviel
gelaufen sein. Der Verlauf der Chromfluoreszenzkurven scheint aber, wie in
Abbildung  zu sehen ist relativ gut mit den Meßwerten bei den
angenommenen Winkeln übereinzustimmen.
zu sehen ist relativ gut mit den Meßwerten bei den
angenommenen Winkeln übereinzustimmen.
Ein Fehler in der Rechnung ist insofern auszuschließen, als daß zumindest
für monochromatische Anregung das Programm überprüft wurde. Allerdings
könnten bei der Integration über die Energie Fehler aufgetreten sein. Das
Maximum des anregenden Synchrotronspektrums lag bei 14 keV. Diese Energie
liegt im Bereich der Gold L-Kanten.
Wie man in Abbildung  erkennen kann, ist in diesem Bereich die
Reflektivität stark durch die Absorption im Gold bestimmt. An den
Absorptionskanten kann es hierdurch leicht zu Fehlern bei der Berechnung der
Reflektivität kommen. Das Maximum der experimentellen Werte bei 5 mrad
entspricht einer anregenden Energie von etwa 18 keV
erkennen kann, ist in diesem Bereich die
Reflektivität stark durch die Absorption im Gold bestimmt. An den
Absorptionskanten kann es hierdurch leicht zu Fehlern bei der Berechnung der
Reflektivität kommen. Das Maximum der experimentellen Werte bei 5 mrad
entspricht einer anregenden Energie von etwa 18 keV
Die Chromschicht hat kaum Einfluß auf die
Goldfluoreszenzintensität. Man kann die Schichtdicke über die relativen
Fluoreszenzintensitäten aus dem Chrom abgeschätzen. Dies ist in
Abbildung
 zu sehen, bei der für eine feste Goldschicht von
7 nm unter Annahme verschiedener Chromschichtdicken die
Cr
zu sehen, bei der für eine feste Goldschicht von
7 nm unter Annahme verschiedener Chromschichtdicken die
Cr 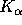 -Strahlung berechnet wurde.
Zum Vergleich sind die relativen Fluoreszenzintensitäten von Chrom aus der
ersten Messung eingetragen.
-Strahlung berechnet wurde.
Zum Vergleich sind die relativen Fluoreszenzintensitäten von Chrom aus der
ersten Messung eingetragen.
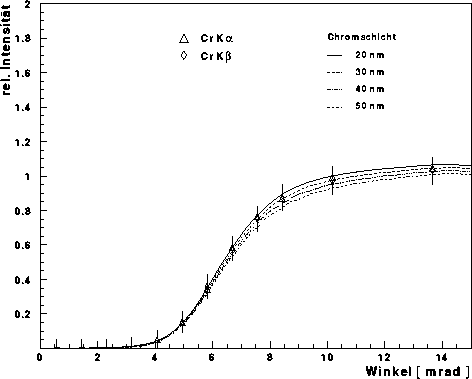
Abbildung: Relative Fluoreszenzintensitäten der Cr 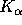 - und
Cr
- und
Cr 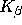 -Linie - Zu
sehen ist die gerechnete relative Fluoreszenzintensität
der Cr
-Linie - Zu
sehen ist die gerechnete relative Fluoreszenzintensität
der Cr 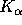 -Linie für eine Goldschicht von 7 nm
und Chromschichten von 20,30,40 bzw. 50 nm. Die eingetragen Werte
stammen aus der ersten Messung. Zur Berechnung der Kurven wurden die Werte
des entsprechenden Kollimators benutzt und eine Strahlbreite von 300 . Die eingetragen Werte
stammen aus der ersten Messung. Zur Berechnung der Kurven wurden die Werte
des entsprechenden Kollimators benutzt und eine Strahlbreite von 300 $
m$ angenommen.
-Linie für eine Goldschicht von 7 nm
und Chromschichten von 20,30,40 bzw. 50 nm. Die eingetragen Werte
stammen aus der ersten Messung. Zur Berechnung der Kurven wurden die Werte
des entsprechenden Kollimators benutzt und eine Strahlbreite von 300 . Die eingetragen Werte
stammen aus der ersten Messung. Zur Berechnung der Kurven wurden die Werte
des entsprechenden Kollimators benutzt und eine Strahlbreite von 300 $
m$ angenommen.
Die Abhängigkeit der Fluoreszenzintensität des Chroms
von der Schichtdicke ist nicht so charakteristisch, wie bei der
Goldschicht. Je dicker die Schicht ist, desto flacher wird die Kurve. Im
betrachteten Winkelbereich liegt kein Intensitätsmaximum. Die Kurve für die
20 nm Chromschicht scheint am besten zu passen. Allerdings ist auch hier zu
bedenken, daß der Verlauf der Kurve von der angenommenen Strahlbreite
abhängt.
Die Goldschicht kann somit mit etwa 6 bis 10 nm abgeschätzt werden und
die Chromschicht mit etwa 20 bis 40 nm. Diese Abschätzung beruht
allein auf relativen Fluoreszenzintensitäten, während bei den oben
erwähnten SYXRF Messungen die absoluten Flächenbelegungen bestimmt worden
sind. Größere
Schwierigkeiten als erwartet, ergaben sich durch die Berücksichtigung
der Strahlbreite bei der relativen Nachweiswahrscheinlichkeit im
Detektor. Die Strahlbreite mußte bei einer horizontalen Blende von
300 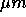 mit 600
mit 600 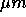 angenommen werden, und schien sich zudem
bei hohen Elektronenströmen zu verbreitern. Es wäre von Vorteil, durch
kürzere Meßzeiten und eine automatisierte Winkeleinstellung zumindest die
Änderung der Strahlbreite während einer Meßreihe zu vermeiden.
angenommen werden, und schien sich zudem
bei hohen Elektronenströmen zu verbreitern. Es wäre von Vorteil, durch
kürzere Meßzeiten und eine automatisierte Winkeleinstellung zumindest die
Änderung der Strahlbreite während einer Meßreihe zu vermeiden.
Die Anregung geschah durch das gesamte Synchrotronspektrum bei einem
Aluminiumabsorber von 0.7 mm. Bei monochromatischer
Anregung würde sich eine schärfere Ausbildung der Kurvenmaxima und -minima
ergeben. Ein andere Möglichkeit wäre es, daß anregende Synchrotronspektrum
durch einen dickeren Aluminiumabsorber weiter aufzuhärten. So würden die
Unsicherheiten bei der Berechnung der Reflektivitäten an den AuL-Kanten
weniger ins Gewicht fallen.




Next: TXRF mit Objektträger
Up: Messungen mit Totalreflexion
Previous: Röntgenspiegel - 'high energy
Anno Hein
Fri Apr 4 12:36:40 CEST 1997



